Table of contents
運動する点電荷が作る電磁場のヘヴィサイド・ファインマン表現とジェフィメンコ方程式
運動する点電荷が作る電場は、リエナー・ブィーヒェルトポテンシャルから導かれた電磁場の式より
\[\mathbf{E} = q \left[ \frac{(1-\beta^2) (\mathbf{n} - \boldsymbol{\beta})}{\kappa^3 R^2}\right] + \frac{q}{c} \left[ \frac{\mathbf{n} \times \{ (\mathbf{n}-\boldsymbol{\beta}) \times \dot{\boldsymbol{\beta}}\} }{\kappa^3 R}\right] \tag{1}\]のように表現されるのでした。以降、これをLW表現と呼ぶことにします。\([ \cdots ]\)部分は遅延時間での物理量を表します。これを求めるのに、私たちは遅延ポテンシャル(LWポテンシャル)を微分したものを計算する必要がありました。しかしファインマン物理学の電磁気学の章には、これを導出するための煩雑な数式変形は掲載されていません。この電磁場は導出するために、ファインマンは以下のような考え方をしたようです。それは、運動していないときに点電荷が作る電場(クーロン電場)に
- 点電荷と観測者の相対位置が変化することによる補正
- 点電荷が加速度運動することによる補正
を加えれば良い、というものです。この言葉を数式として表現すると、次元合わせなどを考慮して
\[\mathbf{E} = q \left[ \frac{\mathbf{n}}{R^2}\right] + q \frac{R}{c} \frac{\partial}{\partial t} \left[ \frac{\mathbf{n}}{R^2}\right] + \frac{q}{c^2} \frac{\partial^2}{\partial t^2} [\mathbf{n}] \tag{2}\]のように書けます。第1項はクーロン電場、第2項は点電荷が速度を持つことによる補正項、第3項は点電荷が加速度運動することによる補正項です。以降、(2)式をヘヴィサイド・ファインマン(HF)表現と呼ぶことにしましょう。
証明
(2)式が(1)式と一致することを示しましょう。遅延時間\(t_\mathrm{ret} = t - \vert \mathbf{r} - \mathbf{r}_0 (t_\mathrm{ret})\vert / c\)より
\[\begin{align} \frac{\partial}{\partial} \left[ \frac{\mathbf{n}}{R^2}\right] &= \frac{\partial t_\mathrm{ret}}{\partial t} \frac{\partial }{\partial t_\mathrm{ret}} \left[ \frac{\mathbf{n}}{R^2}\right] = \left[ \frac{1}{\kappa} \frac{\partial}{\partial t} \left( \frac{\mathbf{R}}{R^3}\right)\right] = \left[ \frac{1}{\kappa} \left( - \frac{3}{R^4} \frac{\partial R}{\partial t} \mathbf{R} + \frac{1}{R^3} \frac{\partial \mathbf{R}}{\partial t}\right)\right] \notag \\ &= \left[ \frac{1}{\kappa} \left\{ \frac{3c}{R^4} (\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{R} - \frac{c}{R^3} \boldsymbol{\beta}\right\}\right] = \left[ \frac{c}{\kappa R^3} \{ 3(\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n} - \boldsymbol{\beta}\}\right] \tag{3} \end{align}\]次に\(\frac{\partial^2}{\partial t^2} [\mathbf{n}]\)の計算を行います。
\[[\dot{\mathbf{n}}] = \left[ \frac{\partial \mathbf{n}}{\partial t}\right] = \left[ \frac{\partial}{\partial t} \frac{\mathbf{R}}{R}\right] = \left[ - \frac{1}{R^2} \frac{\partial R}{\partial t} \mathbf{R} + \frac{1}{R} \frac{\partial \mathbf{R}}{\partial t}\right] = \left[ \frac{c (\mathbf{n} \cdot \boldsymbol{\beta})}{R^2} \mathbf{R} - \frac{c}{R} \boldsymbol{\beta}\right] = \left[ \frac{c}{R} \{(\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n} - \boldsymbol{\beta}\}\right] \tag{4}\] \[\begin{align} [\ddot{\mathbf{n}}] &= \left[ -\frac{c}{R^2} \frac{\partial R}{\partial t} \{ (\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n} - \boldsymbol{\beta}\} + \frac{c}{R} \left\{ (\dot{\mathbf{n}} \cdot \boldsymbol{\beta}) \mathbf{n} + (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \mathbf{n} + (\mathbf{n} \cdot \boldsymbol{\beta}) \dot{\mathbf{n}} - \dot{\boldsymbol{\beta}}\right\}\right] \notag \\ &\underbrace{=}_{(4)} \left[ \frac{c^2}{R^2} (\mathbf{n} \cdot \boldsymbol{\beta}) \{ (\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n} - \boldsymbol{\beta}\} + \frac{c^2}{R^2} \{ (\mathbf{n} \cdot \boldsymbol{\beta})^2 - \beta^2\} \mathbf{n} + \frac{c^2}{R^2} \{ (\mathbf{n}\cdot \boldsymbol{\beta})^2 \mathbf{n} - (\mathbf{n} \cdot \boldsymbol{\beta}) \boldsymbol{\beta}\} + \frac{c}{R} \{ (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \mathbf{n}-\dot{\boldsymbol{\beta}}\}\right] \notag \\ &= \left[ \frac{3 c^2}{R^2} (\mathbf{n} \cdot \boldsymbol{\beta})^2 \mathbf{n} - \frac{2c^2}{R^2} (\mathbf{n}\cdot \boldsymbol{\beta}) \boldsymbol{\beta} - \frac{c^2}{R^2} \beta^2 \mathbf{n} + \frac{c}{R} \{ (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \mathbf{n} - \dot{\boldsymbol{\beta}}\}\right] \tag{5} \end{align}\] \[[\dot{\kappa}] = \left[ \frac{\partial \kappa}{\partial t}\right] = [-\dot{\mathbf{n}} \cdot \boldsymbol{\beta} - \mathbf{n} \cdot \dot{\boldsymbol{\beta}}] \underbrace{=}_{(4)} \left[ - \frac{c}{R} (\mathbf{n} \cdot \boldsymbol{\beta})^2 + \frac{c}{R} \beta^2 - \mathbf{n} \cdot \dot{\boldsymbol{\beta}} \right] \tag{6}\]以上より
\[\begin{aligned} \frac{\partial^2}{\partial t^2} [\mathbf{n}] &= \frac{\partial}{\partial t} \left( \frac{\partial t_\mathrm{ret}}{\partial t} \frac{\partial}{\partial t_\mathrm{ret}} [\mathbf{n}]\right) = \frac{\partial t_\mathrm{ret}}{\partial t} \frac{\partial}{\partial t_\mathrm{ret}} \left[ \frac{\dot{\mathbf{n}}}{\kappa}\right] = \left[ \frac{1}{\kappa} \left( - \frac{\dot{\kappa}}{\kappa^2} \dot{\mathbf{n}} + \frac{\ddot{n}}{\kappa}\right)\right] \\ &= \left[ -\frac{c}{\kappa^3 R} \left\{ -\frac{c}{R} (\mathbf{n} \cdot \boldsymbol{\beta})^2 + \frac{c}{R} \beta^2 - \mathbf{n} \cdot \dot{\boldsymbol{\beta}}\right\} \{ (\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n}-\boldsymbol{\beta}\} \right. \\ & \qquad \left. + \frac{1}{\kappa^2} \left( \frac{3c^2}{R^2} (\mathbf{n}\cdot \boldsymbol{\beta})^2 \mathbf{n} - \frac{2c^2}{R^2} (\mathbf{n} \cdot \boldsymbol{\beta}) \boldsymbol{\beta} - \frac{c^2}{R^2} \beta^2 \mathbf{n} +\frac{c}{R} \left\{ (\mathbf{n}\cdot \dot{\boldsymbol{\beta}}) \mathbf{n} -\dot{\boldsymbol{\beta}}\right\}\right)\right] \end{aligned}\]となります。よって(2)式は
\[\begin{aligned} \mathbf{E} &= q \left[ \frac{\kappa^3}{\kappa^3 R^2} \mathbf{n} + \frac{\kappa^2}{\kappa^3 R^2} \{ 3(\mathbf{n}\cdot \boldsymbol{\beta}) -\boldsymbol{\beta}\} - \frac{1}{\kappa^3 R^2} \{ \beta^2 - (\mathbf{n}\cdot \boldsymbol{\beta})^2\} \{ (\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n} -\boldsymbol{\beta}\} \right. \\ &\qquad \left. + \frac{1}{c\kappa^3 R} (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \{ (\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n}-\boldsymbol{\beta}\} + \frac{\kappa}{\kappa^3 R^2} \{ 3(\mathbf{n}\cdot \boldsymbol{\beta})^2 \mathbf{n} - 2(\mathbf{n} \cdot \boldsymbol{\beta}) \boldsymbol{\beta} - \beta^2 \mathbf{n}\} + \frac{\kappa}{c\kappa^3 R} \{ (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \mathbf{n} -\dot{\boldsymbol{\beta}}\} \right] \end{aligned}\]のように書かれます。全ての項を一度に計算するのは大変なので、(1)式の2つの項を一つずつ計算しましょう。
\[\begin{aligned} \left( \frac{1}{\kappa^3 R^2} の分子\right) &= \kappa^3 \mathbf{n} + \kappa^2 \{ 3(\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n} - \boldsymbol{\beta}\} - \{ \beta^2 - (\mathbf{n} \cdot \boldsymbol{\beta})^2\} \{ (\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n} -\boldsymbol{\beta}\} + \kappa \{ 3(\mathbf{n} \cdot \boldsymbol{\beta})^2 -2(\mathbf{n} \cdot \boldsymbol{\beta}) \boldsymbol{\beta} -\beta^2 \mathbf{n}\} \\ &= \mathbf{n} - 3(\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n} + 3 (\mathbf{n} \cdot \boldsymbol{\beta})^2 \mathbf{n} - (\mathbf{n} \cdot \boldsymbol{\beta})^3 \mathbf{n} + 3(\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n} - 6(\mathbf{n} \cdot \boldsymbol{\beta})^2 \mathbf{n} + 3 (\mathbf{n} \cdot \boldsymbol{\beta})^3 \mathbf{n} - \boldsymbol{\beta} + 2(\mathbf{n} \cdot \boldsymbol{\beta}) \boldsymbol{\beta} \\ & \qquad - (\mathbf{n} \cdot \boldsymbol{\beta})^2 \boldsymbol{\beta} -\beta^2 (\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n} + \beta^2 \boldsymbol{\beta} + (\mathbf{n} \cdot \boldsymbol{\beta})^3 \mathbf{n} - (\mathbf{n} \cdot \boldsymbol{\beta})^2 \boldsymbol{\beta} + 3 (\mathbf{n} \cdot \boldsymbol{\beta})^2 \mathbf{n} - 2(\mathbf{n} \cdot \boldsymbol{\beta}) \boldsymbol{\beta} - \beta^2 \mathbf{n} \\ & \qquad - 3 (\mathbf{n} \cdot \boldsymbol{\beta})^3 \mathbf{n} + 2(\mathbf{n} \cdot \boldsymbol{\beta})^2 \boldsymbol{\beta} + (\mathbf{n} \cdot \boldsymbol{\beta}) \beta^2 \mathbf{n} \\ &= \mathbf{n} - \boldsymbol{\beta} - \beta^2 \mathbf{n} + \beta^2 \boldsymbol{\beta} = (1-\beta^2) (\mathbf{n}-\boldsymbol{\beta}) \end{aligned}\]よって、確かに(1)式の第1項(速度場)に一致します。
\[\begin{aligned} \left( \frac{1}{c \kappa^3 R}の分子\right) &= (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \{ (\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n} - \boldsymbol{\beta}\} + \kappa \{ (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \mathbf{n} -\dot{\boldsymbol{\beta}}\} \\ &= (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) (\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n} - (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \boldsymbol{\beta} + (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \mathbf{n} - (\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) (\mathbf{n} \cdot \boldsymbol{\beta}) \mathbf{n} -\dot{\boldsymbol{\beta}} + (\mathbf{n} \cdot \boldsymbol{\beta}) \dot{\boldsymbol{\beta}} \\ &= (\mathbf{n} \cdot \dot{\beta}) (\mathbf{n}-\boldsymbol{\beta}) - \dot{\boldsymbol{\beta}} + (\mathbf{n}\cdot \boldsymbol{\beta}) \dot{\boldsymbol{\beta}} \\ &= \mathbf{n} \times \{ (\mathbf{n}-\boldsymbol{\beta}) \times \dot{\boldsymbol{\beta}}\} \end{aligned}\]となり、こちらも(1)式の第2項(輻射場)に一致します。
直感的理解
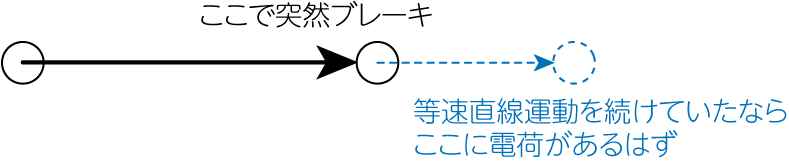
(2)式のようなHF表現で表されると、なぜ加速度運動をしたときにのみ電磁波が出現するかを直感的に理解することができます。下図のように等速直線運動していた点電荷に突然ブレーキをかけて減速させることを考えましょう。このブレーキがなければこの点電荷は等速度で直進していたはずですが、突然のブレーキにより電荷が置いてけぼりとなります。その置いてけぼりとなった部分が電磁波という形で放射されるのです。
ジェフィメンコ方程式
さらに発展させて、任意の電荷分布からの電磁場の放射を考えてみましょう。リエナー・ブィーヒェルトポテンシャルより1つの点電荷により発生する電磁ポテンシャルは
\[\phi = \left[ \frac{q}{\kappa R}\right], \quad \mathbf{A} = \left[ \frac{q \mathbf{u}}{c \kappa R} \right] \tag{7}\]のように書かれるのでした。これを電荷密度分布\(\rho\)、電流密度分布\(\mathbf{j}\)の場合に拡張します。分母に出現する\(\kappa R\)は、速度\(\mathbf{u}(t_\mathrm{ret})\)で運動している際に点電荷が運動することにより生まれる、観測者と点電荷の間の距離\(R\)を補正したものです。
(7)式を任意の電荷密度分布に対し空間の全領域で積分し重ね合わせたものが、求めたい電荷分布が作る遅延ポテンシャルです。観測者は十分遠方にいると仮定すると、距離による補正は\(\kappa \sim 1\)のように考えることができます。よって
\[\phi(\mathbf{r}, t) = \iiint \frac{[\rho]}{R} dV, \quad \mathbf{A} (\mathbf{r}, t) = \iiint \frac{[\mathbf{j}]}{cR} dV \tag{8}\]が求めたい遅延ポテンシャルとなります。これらを
\[\mathbf{E} = - \nabla \phi - \frac{1}{c} \frac{\partial \mathbf{A}}{\partial t}, \quad \mathbf{B} = \nabla \times \mathbf{A}\]に代入して計算を行えば電磁場が得られます。
\[\frac{\partial}{\partial r_i} [\rho] = \frac{\partial t_\mathrm{ret}}{\partial r_i} \left[ \frac{\partial \rho}{\partial t}\right] = - \frac{R_i}{cR} \left[ \frac{\partial \rho}{\partial t}\right]\]より
\[(\nabla \phi)_i = \frac{\partial \phi}{\partial r_i} = \iiint \frac{- \frac{R_i}{cR} \left[ \frac{\partial \rho}{\partial t} \right] R - \rho \frac{R_i}{R}}{R^2} dV = - \iiint \left( \frac{1}{cR} \left[ \frac{\partial \rho}{\partial t} \right] + \frac{\rho}{R^2} \right) n_i dV\] \[\frac{\partial \mathbf{A}}{\partial t} = \iiint \frac{\partial}{\partial t} \frac{[\mathbf{j}]}{cR} dV = \iiint \frac{1}{cR} \frac{\partial t_\mathrm{ret}}{\partial t} \left[ \frac{\partial \mathbf{j}}{\partial t} \right] dV = \iiint \frac{1}{cR} \left[ \frac{\partial \mathbf{j}}{\partial t} \right] dV\]などをあらかじめ計算しておきます。ここで\(t_\mathrm{ret} = t - \vert \mathbf{r} -\mathbf{r}_0\vert / c\)より、本来なら\(\mathbf{r}_0\)の時間変化による効果が入りますが、ここでは\(r_0 \ll r\)と近似することで\(\frac{\partial t_\mathrm{ret}}{\partial t} \sim 1\)としました。
\[\mathbf{E} = \iiint \left( \frac{[\rho]}{R^2} \mathbf{n} + \frac{1}{cR} \left[ \frac{\partial \rho}{\partial t} \right] \mathbf{n} - \frac{1}{c^2 R} \left[ \frac{\partial \mathbf{j}}{\partial t}\right] \right) dV \tag{9}\] \[\mathbf{B} = \iiint \left( \frac{[\mathbf{j}]}{cR^2} \times \mathbf{n} + \frac{1}{c^2R} \left[ \frac{\partial \mathbf{j}}{\partial t} \right] \times \mathbf{n} \right) dV \tag{10}\]と求まります。(9), (10)式をジェフィメンコ方程式(Jefimenko’s equations)と呼びます。(9)式の第1項はクーロンの法則、(10)式の第1項はビオ・サバールの法則を表しています。これらのよく知られた電磁気の法則を拡張したものがジェフィメンコ方程式です。静電場・静磁場に補正を加えることで得たHF表現と同じような形をしています。
さらにこれを解析しやすい形に直しましょう。電荷の位置\(\mathbf{r}_0\)での電流密度\([\mathbf{j}]\)の発散を計算することを考えます。
ですが、実際には\(\mathbf{j}\)は\(t_\mathrm{ret}\)を通じて\(\mathbf{r}\)にも依存しています。よって連鎖律より
\[\frac{\partial}{\partial r_{0, i}} = \left( \frac{\partial}{\partial r_{0, i}}\right)_\mathbf{r} + \frac{\mathbf{n}}{c} \frac{\partial}{\partial t_\mathrm{ret}}\]となります。ここで位置\(\mathbf{r}_0\)から観測者のいる\(\mathbf{r}\)の方向を向く単位ベクトルを\(\mathbf{n} = \mathbf{R} / R\)としました。以上から
\[\frac{\partial}{\partial r_{0, i}} [j_i] = \left[ \frac{\partial j_i}{\partial r_{0, i}}\right] + \frac{n_i}{c} \left[ \frac{\partial j_i}{\partial t}\right]\]ここで電荷分布と電流分布に対する連続の式
\[\frac{\partial \rho}{\partial t} + \nabla \cdot \mathbf{j} = 0\]より
\[\nabla \cdot [\mathbf{j}] = -\left[ \frac{\partial \rho}{\partial t} \right] + \frac{\mathbf{n}}{c} \cdot \left[ \frac{\partial \mathbf{j}}{\partial t}\right] \ \underbrace{\Longrightarrow}_{\times \mathbf{n}/cR} \ \frac{1}{cR} \left[ \frac{\partial \rho}{\partial t}\right] \mathbf{n} = -\frac{1}{cR} (\nabla \cdot [\mathbf{j}]) \mathbf{n} + \left( \frac{\mathbf{n}}{c^2 R} \cdot \left[ \frac{\partial \mathbf{j}}{\partial t}\right] \right) \mathbf{n}\]以上の変形と(9)式より
\[\mathbf{E} = \iiint \left\{ \frac{[\rho]}{R^2} \mathbf{n} - \frac{1}{cR} (\nabla \cdot [\mathbf{j}]) \mathbf{n} + \frac{1}{c^2 R} \left( \mathbf{n} \cdot \left[ \frac{\partial \mathbf{j}}{\partial t}\right] \right) \mathbf{n} - \frac{1}{c^2R} \left[ \frac{\partial \mathbf{j}}{\partial t}\right]\right\} dV \tag{11}\]第2項の\(k\)成分を計算します。
\[\frac{1}{cR} \frac{\partial [j_i]}{\partial r_{0, i}} n_k = \frac{1}{cR} \frac{\partial}{\partial r_{0, i}} \left( \frac{[j_i] n_k}{R}\right) - \frac{[j_i]}{c} \frac{\partial}{\partial r_{0, i}} \left( \frac{n_k}{R}\right) = \frac{1}{cR} \frac{\partial}{\partial r_{0, i}} \left( \frac{[j_i] R_k}{R^2}\right) - \frac{[j_i]}{c} \frac{\partial}{\partial r_{0, i}} \left( \frac{R_k}{R^2}\right)\]\(\mathbf{R} = (x-x_0, y-y_0, z-z_0)\)より
\[\frac{\partial}{\partial r_{0, i}} \left( \frac{R_k}{R^2}\right) = \frac{-\delta_{ik} R^2 - R_k (-2R_i)}{R^4}\]のように計算されます。よって最終的に
\[\frac{1}{cR} \frac{\partial [j_i]}{\partial r_{0, i}} n_k = \frac{1}{c} \frac{\partial}{\partial r_{0, i}} \left( \frac{R_k}{R^2} [j_i]\right) - \frac{-[j_k] + 2([\mathbf{j}] \cdot \mathbf{n}) n_k}{cR^2}\]を得ます。この第一項はベクトルの発散の形で書かれています。これが(9)式の体積積分の中に入っているため、ガウスの定理より表面積分に書き直されます。電荷や電流の存在しない無限遠を表面にとれば、この部分は0になるとわかります。よってこの第二項の計算だけ進めていきましょう。ここでベクトル恒等式より
\[\begin{aligned} [(\mathbf{a} \times \mathbf{n}) \times \mathbf{n}]_i &= \epsilon_{ijk} (\mathbf{a} \times \mathbf{n})_j n_k = \epsilon_{ijk} \epsilon_{j\ell m} a_\ell n_m n_k = \epsilon_{jki} \epsilon_{j \ell m} a_\ell n_m n_k = (\delta_{k\ell} \delta_{im} - \delta_{km} \delta_{i\ell}) a_\ell n_m n_k \\ &= a_k n_i n_k - a_i n_k n_k = (\mathbf{a} \cdot \mathbf{n}) n_i - a_i \end{aligned}\]です。ここで\(n_i = R_i /R\)のように規格化されているとしました。すると
\[- \frac{-[\mathbf{j}] + 2([\mathbf{j}] \cdot \mathbf{n}) \mathbf{n}}{cR^2} = - \frac{([\mathbf{j}] \cdot \mathbf{n}) \mathbf{n} + ([ \mathbf{j}] \times \mathbf{n}) \times \mathbf{n}}{cR^2}\]のようになります。以上から
\[\frac{1}{cR} (\nabla \cdot [\mathbf{j}]) \mathbf{n} = - \frac{([\mathbf{j}] \cdot \mathbf{n}) \mathbf{n} + ([\mathbf{j}] \times \mathbf{n}) \times \mathbf{n}}{cR} \tag{12}\]さらに(11)式の第3, 4項は、先程のベクトル恒等式を用いれば
\[\frac{1}{c^2R} \left\{ \left( \mathbf{n} \cdot \left[ \frac{\partial \mathbf{j}}{\partial t}\right]\right) \mathbf{n} - \left[ \frac{\partial \mathbf{j}}{\partial t}\right]\right\} = \frac{1}{c^2 R} \left( \left[ \frac{\partial \mathbf{j}}{\partial t}\right] \times \mathbf{n}\right) \mathbf{n} \tag{13}\]のように書かれます。(11), (12), (13)式より、最終的に
\[\mathbf{E} = \iiint \left\{ \frac{[\rho]}{R^2} \mathbf{n} + \frac{([\mathbf{j}] \cdot \mathbf{n}) \mathbf{n}}{cR^2} + \frac{([\mathbf{j}] \times \mathbf{n}) \times \mathbf{n}}{cR^2} + \frac{1}{c^2 R} \left( \left[ \frac{\partial \mathbf{j}}{\partial t}\right] \times \mathbf{n}\right) \times \mathbf{n} \right\} dV \tag{14}\](14)式の第1, 2項は\(\mathbf{n}\)に平行な成分、第3, 4項は\(\mathbf{n}\)に垂直な成分です。中でも第4項は\(R^{-1}\)に比例する項なので、\(R \rightarrow \infty\)ではこの項のみが支配的となります。無限遠にもエネルギーを持ち去ることができるこの項が電磁放射に対応します。電磁放射の成分のみを書くと
\[\mathbf{E} = \iiint \left\{ \frac{1}{c^2 R} \left( \left[ \frac{\partial \mathbf{j}}{\partial t}\right] \times \mathbf{n}\right) \times \mathbf{n} \right\} dV \tag{15}\] \[\mathbf{B} = \iiint \left\{ \frac{1}{c^2R} \left[ \frac{\partial \mathbf{j}}{\partial t} \right] \times \mathbf{n} \right\} dV = \mathbf{n} \times \mathbf{E} \tag{16}\]となります。
参考文献
- 宮島龍興, “ファインマン物理学3 電磁気学”