Table of contents
湯川型ポテンシャルの導出
デバイ・ヒュッケルの理論で出現した以下のポテンシャルを、もとの方程式から求めてみましょう。 ここでは\(\mu = 1/\lambda_D\)とした、以下の方程式の解を求めます。
\[\left( \Delta - \mu^2 \right) \phi = - 4\pi q_0 \delta^3(\mathbf{r}) \tag{1}\]フーリエ変換による方法
今回はフーリエ変換の方法を用いて解きます。 左辺の\(\phi\)の逆フーリエ変換を考えると
\[(\Delta - \mu^2) \iiint_{-\infty}^\infty \hat{\phi}(\mathbf{k}) e^{i \mathbf{r} \cdot \mathbf{k}} d^3 \mathbf{k} = \iiint_{-\infty}^\infty \hat{\phi} (\mathbf{k}) (\Delta-\mu^2) e^{i \mathbf{r} \cdot \mathbf{k}} d^3 \mathbf{k} = \iiint_{-\infty}^\infty \hat{\phi} (\mathbf{k}) (-k^2-\mu^2) e^{i \mathbf{r} \cdot \mathbf{k}} d^3 \mathbf{k} \tag{2}\]これと、右辺のデルタ関数の積分表示より
\[\iiint_{-\infty}^\infty \hat{\phi} (\mathbf{k}) (-k^2-\mu^2) e^{i \mathbf{r} \cdot \mathbf{k}} d^3 \mathbf{k} = - \frac{4\pi q_0}{(2\pi)^3} \iiint_{-\infty}^\infty e^{i \mathbf{r} \cdot \mathbf{k}} d^3 \mathbf{k} \tag{3}\]両辺を比較することで
\[\hat{\phi} (\mathbf{k}) = \frac{q_0}{2\pi^2} \frac{1}{k^2 + \mu^2} \tag{4}\]を得ます。 逆フーリエ変換したものが求まったので、これをフーリエ変換すればそれが(1)式の解になります。 積分の取り方としては、\(\mathbf{r} \cdot \mathbf{k} = rk \cos \theta\)のように、\(\mathbf{r}\)からの偏角を用いた極座標設定にすると計算が便利です。
\[\begin{align} \phi(\mathbf{r}) &= \frac{q_0}{2\pi^2} \iiint_{-\infty}^\infty \frac{e^{i\mathbf{r} \cdot \mathbf{k}}}{k^2 + \mu^2} d^3 \mathbf{k} \underbrace{=}_{d^3 \mathbf{k}= k^2 \sin \theta dk d\theta d\varphi} \frac{q_0}{2\pi^2} \int_0^\infty dk \int_0^\pi \int_0^{2\pi} d\varphi e^{ikr \cos \theta} \frac{k^2}{k^2 + \mu^2} \sin \theta \notag \\ &\underbrace{=}_{\nu = \cos \theta} \frac{q_0}{\pi} \int_0^\infty dk \int_{-1}^1 d\nu e^{irk\nu} \frac{k^2}{k^2 + \mu^2} = \frac{q_0}{\pi} \int_0^\infty \frac{k^2}{k^2 + \mu^2} \frac{e^{irk} - e^{-irk}}{irk} dk \notag \\ &= \frac{2q_0}{\pi r} \int_0^\infty \frac{k \sin rk}{k^2 + \mu^2} dk \tag{5} \end{align}\]最後に出てきた被積分関数は偶関数であるため、以下のように変形することができます。
\[\phi (r) = \frac{q_0}{\pi r} \int_{-\infty}^\infty \frac{k \sin rk}{k^2 + \mu^2} dk = \frac{q_0}{2i \pi r} \int_{-\infty}^\infty \frac{k}{k^2 + \mu^2} (e^{irk} - e^{-irk}) dk \tag{6}\]複素平面上での積分
(6)式の積分を計算するために
\[f(z) = \frac{z}{z^2 + \mu^2} e^{irz} \quad (z = x+ iy) \tag{7}\]を、下図左パネルの複素平面上の閉曲路で積分することを考えましょう。
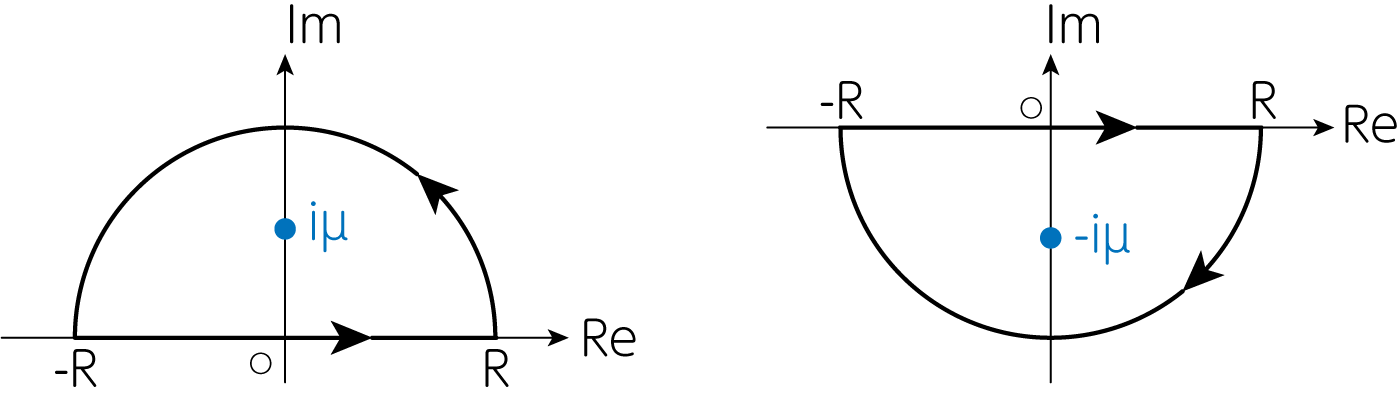
ただし、\(R > \mu\)とします。 留数定理より
\[\oint_{C_1 + C_2} f(z) dz = 2\pi i \mathrm{Res} (f; i\mu) \tag{9}\]です。 ここで\(\mathrm{Res} (f; i\mu)\)は、関数\(f(z)\)の\(z = i\mu\)における留数(residue)を表すものです。 留数を求めるために、\(f(z)\)を変形しましょう。
\[f(z) = \frac{z}{z^2 + \mu^2} e^{irz} = \frac{1}{2} \left( \frac{1}{z-i\mu} + \frac{1}{z+ i\mu} \right) e^{irz} \tag{10}\]\(e^{irz}\)を\(z = i\mu\)の周りでテイラー展開すると
\[e^{irz} = e^{-r\mu} + ir e^{-r\mu} (z-i\mu) + ((z-i\mu)の2次以上の項)\]のようになるため、
\[f(z) = \frac{1}{2} \frac{e^{-r\mu}}{z-i\mu} + \frac{1}{2} ir e^{-r\mu} + ((z-i\mu)の1次以上の項) + \frac{1}{2} \frac{e^{irz}}{z+i\mu} \tag{11}\]を得ます。 右辺において第一項以外は\(z=i\mu\)で正則なので
\[\mathrm{Res}(f; i\mu) = \frac{1}{2} e^{-r\mu} \tag{12}\]となります。 (9), (12)式より
\[\int_{-R}^R f(x) dx + \int_{C_2} f(z) dz = i\pi e^{-r\mu} \ \underbrace{\Longrightarrow}_{R \rightarrow \infty} \ \int_{-\infty}^\infty f(x) dx = i\pi e^{-r\mu} - \lim_{R \rightarrow \infty} \int_{C_2} f(z) dz \tag{13}\](13)式の極限部分の値を求めましょう。 \(C_2\)上では\(z = R e^{i\theta}, dz = iR e^{i\theta} d\theta\)より
\[\begin{align} \lim_{R\rightarrow \infty} \left| \int_{C_2} f(z) dz \right| &= \lim_{R\rightarrow \infty} \left| \int_0^\pi iR e^{i\theta} \frac{R e^{i\theta}}{R^2 e^{2i\theta} + \mu^2} e^{irR e^{i\theta}} d\theta \right| \notag \\ &\leq \lim_{R\rightarrow \infty} \int_0^\pi \left| \frac{i R^2 e^{2i\theta}}{R^2 e^{2i\theta} + \mu^2}\right| \left| e^{irR\cos \theta} e^{-rR\sin \theta}\right| d\theta \notag \\ &\leq \lim_{R \rightarrow \infty} \int_0^\pi \frac{R^2}{R^2 - \mu^2} e^{-rR \sin \theta} d\theta \tag{14} \end{align}\]のように大きさを評価することができます。 最後の指数部分において、\(0 \leq \sin \theta \leq 1 \ (0 \leq \theta \leq \pi)\)より、この極限値は0となります。 よって
\[\int_{-\infty}^\infty f(x) dx = i\pi e^{-r \mu} \tag{15}\]と求まります。 同様に(6)式の第二項を計算するために
\[g(z) = \frac{z}{z^2 + \mu^2} e^{-irz} \quad (z = x + iy) \tag{16}\]を、上図右パネルの複素平面上の閉曲路で積分を行います。 この場合は\(z= -i\mu\)での留数を考えて計算を行うこと、そして経路が時計回りであることから符号に注意すると、次のようになります。
\[\int_{-\infty}^\infty g(x) dx = -i\pi e^{-r\mu} \tag{17}\](6), (15), (17)式より
\[\phi (r) = \frac{q_0}{r} e^{-\mu r} \tag{18}\]のようになります。 比較のために、普通のクーロンポテンシャル\(\phi(r) = q_0 / r\)とともに図示したグラフを示します。 このグラフでは\(q_0 = 1, \mu = 1\)として可視化しています。
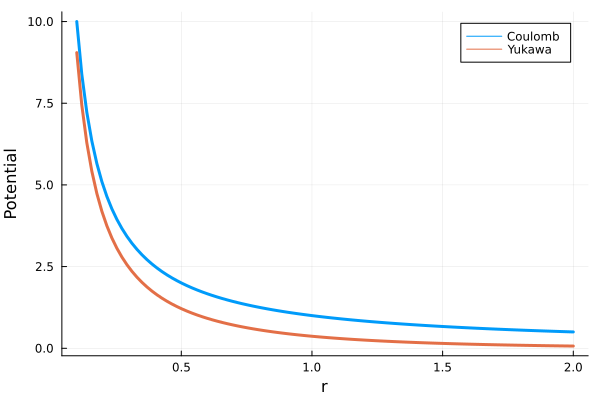
青線はクーロンポテンシャル、橙線は湯川型ポテンシャルです。 (18)式からも明らかですが、湯川型ポテンシャルはクーロンポテンシャルよりも素早く減衰します。 \(r=1/\mu = 1.0\)ではクーロンポテンシャルの\(1/e\)倍になります。 このことから\(r=1/\mu\)程度が、ポテンシャルの影響がある範囲と見ることができます。
デバイ・ヒュッケルの理論から導かれた、弱結合プラズマ中での静電ポテンシャル\(\phi (r) = \frac{q_0}{r} e^{-r/\lambda_D}\)では、\(r = \lambda_D\)程度しかポテンシャルの影響がないことがわかります。 当然ながら、\(\mu = 1/\lambda_D = 0\)ではクーロンポテンシャルと等しくなります。 これは、元の数式である(1)式が
のように、真空中で点電荷を原点に置いた場合に一致することからもわかります。
補遺: Juliaスクリプト
using Plots
gr()
len = 100
r = range(0.1, 2.0, length=len)
coulomb = 1.0 ./ r
yukawa = exp.(-r) ./ r
plot(r, coulomb, linewidth=3, xlabel="r", ylabel="Potential", label="Coulomb")
plot!(r, yukawa, linewidth=3, label="Yukawa")
savefig("yukawa_pot_02.png")
参考文献
[1] Chen, “プラズマ物理入門”
[2] 小野高幸, 三好由純, “太陽地球圏”
[3] 田中基彦, 西川恭治, “高温プラズマの物理学”