Table of contents
逆Compton散乱
下図のように運動している電子によって光子が散乱された場合を考えましょう。以下、実験室系(電子が動いて見える系)をK系、衝突前の電子静止系をK’系とします。
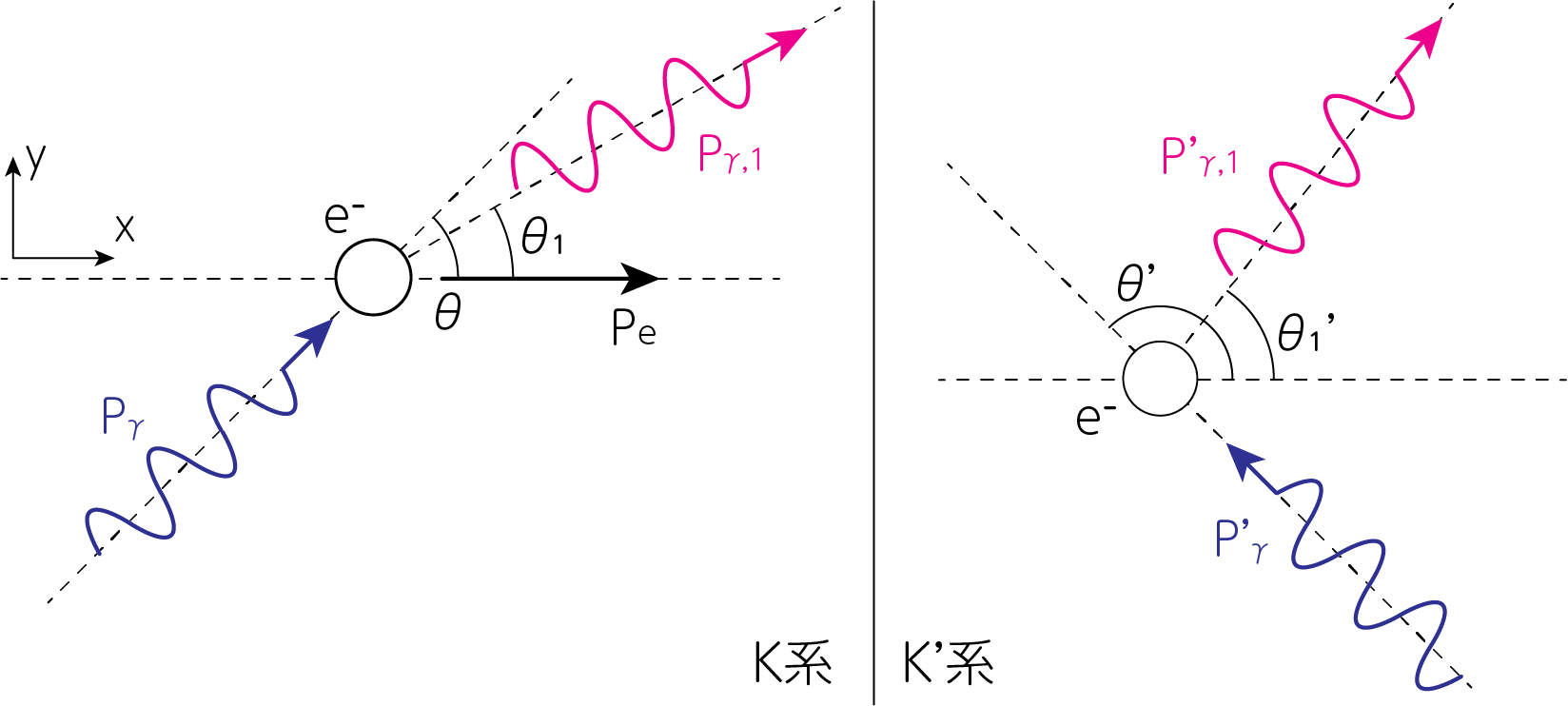
そしてK’系の物理量には’をつけることにします。またK’系では\(\epsilon' \ll m_e c^2\)(入射光子のエネルギーは電子の質量エネルギーよりも十分小さい)とします。K系での散乱前の電子は\(x\)方向に速度\(v\)で運動しているものとします。ここで\(\epsilon, \epsilon_1\)はそれぞれ散乱前後の光子のエネルギーです。
Doppler shift
K系で速度\(v\)で運動する電子が放射する電磁波について考えましょう。時刻\([t, t+dt]\)間に放出した電磁波を、K系に静止した観測者は\([t_\mathrm{obs}, t_\mathrm{obs} + dt_\mathrm{obs}]\)に受け取ったとしましょう。時刻\(t\)における電子と観測者の距離を\(L\)とすると
\[t_\mathrm{obs} = t+ \frac{L}{c}\]観測者が無限遠におり、\(dt\)が微小と考えると、電子から観測者の方向を向く単位ベクトル\(\mathbf{n}\)に変化はないとして
\[t_\mathrm{obs} + dt_\mathrm{obs} = t + dt + \left( \frac{L}{c} - \frac{\mathbf{n} \cdot \mathbf{v}dt}{c} \right)\]以上より
\[dt_\mathrm{obs} = dt- \frac{\mathbf{n}\cdot \mathbf{v} dt}{c} = (1-\mathbf{n} \cdot \boldsymbol{\beta}) dt \tag{1}\]です。これはDopper shiftを表します。
Lorentz変換
\(dt\)をK’系で測定した時間間隔\(dt'\)とすると、両者の関係はLorentz変換より
\[\left( \begin{array}{c} ct' \\ x' \end{array} \right) = \left( \begin{array}{cc} \gamma & -\gamma \beta \\ -\gamma \beta & \gamma \end{array} \right) \left( \begin{array}{c} ct \\ x \end{array} \right) = \left( \begin{array}{c} \gamma ct -\gamma \beta x \\ -\gamma \beta c t + \gamma x \end{array} \right)\]電子と一緒に速度\(v\)で移動する系に移っているので、\(x'=0\)(常に電子は原点で静止して見える)です。これより
\[\left\{ \begin{array}{l} ct' = \gamma ct -\gamma \beta x \\ x=\beta ct \end{array} \right. \ \Longrightarrow \ t ' = \gamma t - \gamma \beta^2 t = \gamma t (1- \beta^2) = \frac{t}{\gamma} \tag{2}\]実験室系・電子静止系の間に成り立つエネルギーの関係式
上図のようにK系において観測者が光子の直進方向にいるとき、すなわち\(\mathbf{n} \cdot \boldsymbol{\beta} = \beta \cos \theta\)のとき
\[\epsilon = h \nu = \frac{h}{dt_{\rm obs}} = \frac{h}{(1- \beta \cos \theta) dt} = \frac{1}{\gamma (1-\beta \cos \theta)} \frac{h}{dt'} = \frac{1}{\gamma (1-\beta \cos \theta)} h \nu' = \frac{1}{\gamma (1-\beta \cos \theta)} \epsilon'\]ここで\(dt\)は放出された電磁波の1周期と考えました。よって
\[\epsilon' = \gamma (1-\beta \cos \theta) \epsilon \tag{3}\]同様にK’系において観測者が散乱後の光子の直進方向にいるとき、すなわち\(\mathbf{n}_1' \cdot \boldsymbol{\beta} = -\beta \cos \theta_1'\)のときを考えます。散乱後の物理量に1の添字をつけて表現すると
\[\epsilon_1' = h \nu_1' = \frac{h}{dt_{\rm obs1}'} = \frac{h}{(1 + \beta \cos \theta_1') dt_1'}\]今度は電子と一緒の速度\(v\)で移動するK’系から観測者が静止しているK系に移ることを考えます。(2)式の関係が逆転するだけなので\(dt_1 = dt_1'/\gamma\)より
\[\epsilon_1' = \frac{1}{\gamma (1+ \beta \cos \theta_1')} \frac{h}{dt_1} = \frac{1}{\gamma (1+ \beta \cos \theta_1')} h \nu_1 = \frac{1}{\gamma (1+ \beta \cos \theta_1')} \epsilon_1\]以上より
\[\epsilon_1 = \gamma (1+ \beta \cos \theta_1') \epsilon_1' \tag{4}\]Compton散乱
K’系では電子は静止しています。よってこれはCompton散乱の式が成立します。
\[\epsilon_1' = \frac{\epsilon'}{1+ \frac{\epsilon'}{m_e c^2} (1- \cos \Theta)} \underbrace{\simeq }_{\epsilon' \ll m_e c^2} \epsilon' \left\{ 1- \frac{\epsilon'}{m_e c^2} (1- \cos \Theta) \right\} \simeq \epsilon' \tag{5}\]ただし、\(\cos\)の中身が\(\theta\)とは異なることに注意しましょう。元々、Compton散乱に出現する\(\cos \theta\)は散乱前後の光子の運動方向と平行な単位ベクトルの内積
\[\mathbf{n} \cdot \mathbf{n}_1 = (1, 0, 0) \cdot (\cos \theta, \sin \theta, 0) = \cos \theta\]から出てきたものです。よってこの\(\cos \Theta\)による置き換えは、K’系での単位ベクトル\(\mathbf{n}', \mathbf{n}_1'\)の内積を実際に計算しなければなりません。
\[\left\{ \begin{array}{l} \mathbf{n}' = (\cos \theta', \sin \theta' \cos \phi', \sin \theta' \sin \phi') \\ \mathbf{n}_1' = (\cos \theta_1', \sin \theta_1' \cos \phi_1', \sin \theta_1' \sin \phi_1') \end{array} \right.\]とすると
\[\begin{align} \mathbf{n}' \cdot \mathbf{n}_1' &= \cos \theta' \cos \theta_1' + \sin \theta' \cos \phi' \sin \theta_1' \cos \phi_1' + \sin \theta' \sin \phi' \sin \theta_1' \sin \phi_1' \notag \\ &= \cos \theta' \cos \theta_1' + \sin \theta' \sin \theta_1' (\cos \phi' \cos \phi_1' + \sin \phi' \sin \phi_1') \notag \\ &= \cos \theta' \cos \theta_1' + \sin \theta' \sin \theta_1' \cos (\phi' - \phi_1' ) = \cos \Theta \tag{6} \end{align}\]光子のエネルギー変化
(4), (5)式より
\[\epsilon_1 = \gamma (1+ \beta \cos \theta_1') \epsilon_1' \simeq \gamma (1+ \beta \cos \theta_1') \epsilon' = \gamma^2 (1+ \beta \cos \theta_1') (1-\beta \cos \theta) \epsilon \tag{7}\]以降では、特に\(\theta=\pi, \theta'_1=0\)(相対論的な電子と光子が正面衝突した)のときを考えましょう。すると
\[\epsilon_1 \simeq \gamma^2 (1+ \beta)^2 \epsilon\]のように、光子のエネルギー変化\(\Delta \epsilon = \epsilon_1 - \epsilon\)が最大となります。
電子のLorentz因子が\(\gamma \gg 1\)であるとすると、\(\beta \sim 1\)より
となり、\(\gamma^2\)に比例してエネルギーを獲得することがわかります。
また非相対論的\(\gamma \sim 1, \beta \ll 1\)の場合は
よりエネルギー変化分は
\[\Delta \epsilon \simeq 2 \beta \epsilon \tag{9}\]のようになります。
実際の例
\(\epsilon = 3 \times 10^{-4}\)eVの光子が電子と衝突して、光子のエネルギーが\(\epsilon_1 \sim 10\)keVになったとすると、電子のLorentz因子はどの程度でしょうか。\(3 \times 10^{-4}\)eVというのはおよそ3K、すなわちここでは宇宙マイクロ波背景放射(CMB)光子を想定しています。(8)式より
\[\frac{10 \mathrm{keV}}{3 \times 10^{-4} \mathrm{eV}} = \frac{10^8}{3} = 4\gamma^2 \ \Longrightarrow \ \gamma \sim 3 \times 10^3\]\(\epsilon, \epsilon_1\)さえわかれば、逆Compton散乱を起こす電子の速度がわかります。
次に\(\epsilon=3 \times 10^{-4}\)eVの光子が\(k_B T = 5\)keVで熱運動する電子と正面衝突した場合のエネルギー変化はどうなるでしょうか。今、\(k_B T \ll m_e c^2\)より、この熱運動電子の運動は非相対論的なので、(9)式を用いて計算をしましょう。熱エネルギーと運動エネルギーの間で等分配が起こっていると仮定すると
これと(9)式より
\[\Delta \epsilon \sim 2 \epsilon \sqrt{\frac{3 k_B T}{m_e c^2}} \sim 1 \times 10^{-4} [\mathrm{eV}]\]となります。ここで出てきた\(5 \mathrm{keV} (= 5 \times 10^7 \mathrm{K})\)は銀河団プラズマの温度程度です(近傍銀河団ではVirgo clusterがおよそ2-3keV, Coma clusterがおよそ8-9keV程度です)。