Table of contents
微粒子による散乱
微粒子などに電磁波が入射すると、その入射電磁波は荷電粒子と相互作用を起こし、散乱されることはよく知られています。 この散乱現象は、入射電磁波の波長と微粒子の大きさによって、その様子が変わります。 大雑把には、以下の3つの分類に分けられます。
- 微粒子の大きさが電磁波の波長よりもすごく小さい: レイリー散乱 (Rayleigh scattering)
- 微粒子の大きさと電磁波の波長が同程度: ミー散乱 (Mie scattering)
- 微粒子の大きさが電磁波の波長よりもすごく大きい: 回折による散乱
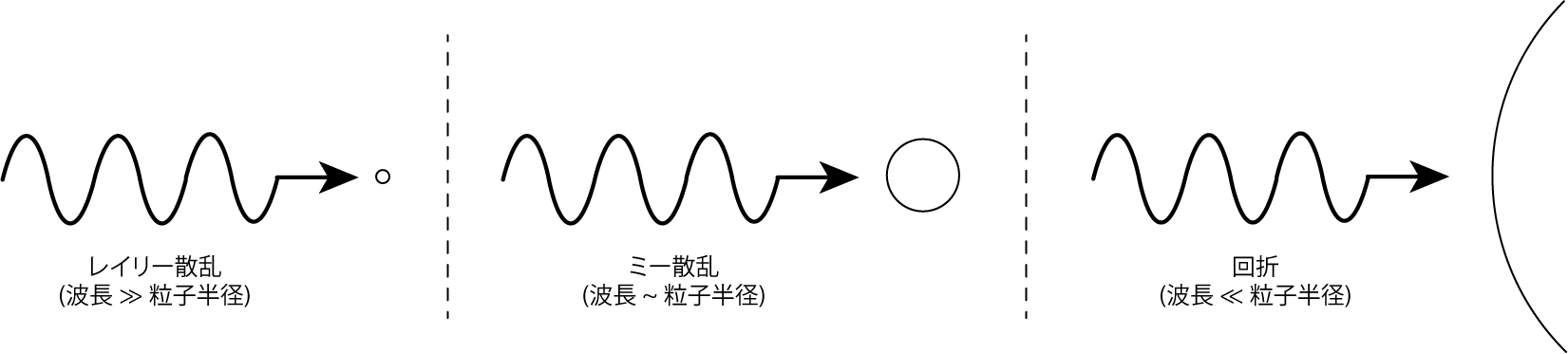
以下では、微粒子の大きさが電磁波波長よりも小さい極限である、レイリー散乱について学びましょう。 このレイリー散乱は、空が青い理由、そして夕焼けが赤い理由としても有名な散乱現象です。
誘電体球による電磁波の散乱
一様電場中の誘電体球
さて、ここからは微粒子について考えていきましょう。 簡単のため、微粒子を半径\(a\)、誘電率\(\varepsilon_1\)の一様な誘電体球と近似します。 この誘電体球に、\(z\)軸方向を向いた一様電場\(E_0\)をかけます。 誘電体球の正味の電荷はゼロであるとします。 さらに誘電体球外部は真空であり、その誘電率を\(\varepsilon_0\)とします。
外場として与えた電場の静電ポテンシャルは、以下のように書けます。
次に誘電体球内部の静電ポテンシャルを\(\Phi_1\)、外部の静電ポテンシャルを\(\Phi_2\)とします。 特に外部の静電ポテンシャルのうち、誘電体球の存在によって誘起される静電ポテンシャル成分を\(\Phi_\mathrm{P}\)のように書きましょう。 誘電体球外部の静電場は、外部から与えた電場と誘電体球が作る電場の重ね合わせとなり、\(\Phi_2 = \Phi_0 + \Phi_\mathrm{P}\)のように書けます。 誘電体球表面でのポテンシャルの連続性より
\[\Phi_1 (a, \theta, \varphi) = - E_0 a \cos \theta + \Phi_\mathrm{P} (a, \theta, \varphi) \tag{2}\]この式が任意の\(\theta, \varphi\)に対して成り立つためには、ポテンシャルの形が以下のようであれば良いでしょう。
\[\Phi_i = F_i(r) \cos \theta \qquad (i = 1, \mathrm{P}) \tag{3}\]静電ポテンシャルは、ラプラス方程式
\[\Delta \Phi_i = \frac{1}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial \Phi_i }{\partial r}\right) + \frac{1}{r^2 \sin \theta} \frac{\partial}{\partial \theta} \left( \sin \theta \frac{\partial \Phi_i}{\partial \theta}\right) = 0\tag{4}\]を満たすため、この方程式に(3)式を代入すれば、\(F_i\)が満たす方程式を得ることができます。
\[\frac{1}{r^2} \frac{d}{d r} \left( r^2 \frac{d F_i}{d r}\right) - \frac{2 F_i}{r^2} = 0 \tag{5}\]この方程式の独立な解は
\[F_i (r) = r, \ r^{-2} \tag{6}\]の2つです。無限遠での境界条件\(\lim_{r \rightarrow \infty} \Phi_\mathrm{P} = 0\)と、原点で\(\Phi_1\)が有限であるという要請から
\[\Phi_1 (r) = C_1 r \cos \theta , \quad \Phi_\mathrm{P} (r) = \frac{C_\mathrm{P}}{r^2} \cos \theta \tag{7}\]となります。 ここで\(C_1, C_\mathrm{P}\)は別の境界条件から求まる定数です。 (2)式より
\[C_1 a \cos \theta = - E_0 a \cos \theta + \frac{C_\mathrm{P}}{a^2} \cos \theta \tag{8}\]さらに、誘電体球表面に垂直な電束密度成分の連続性から
\[\varepsilon_1 \frac{\partial \Phi_1}{\partial r} = \varepsilon_0 \frac{\partial \Phi_2}{\partial r} \ \Longrightarrow \ \varepsilon_1 C_1 \cos \theta = \varepsilon_0 \left( -E_0 - \frac{2C_\mathrm{P}}{a^3} \right) \cos \theta \tag{9}\]が成り立ちます。 (8), (9)式の辺々割り算を行うと
\[\frac{a}{\varepsilon_1} = \frac{- E_0 a + \frac{C_\mathrm{P}}{a^2}}{-\varepsilon_0 \left( E_0 + \frac{2 C_\mathrm{P}}{a^3}\right)} \ \Longrightarrow \ C_\mathrm{P} = \frac{\varepsilon_1 - \varepsilon_0}{\varepsilon_1 + 2 \varepsilon_0} a^3 E_0 \tag{10}\]と求まります。 そして
\[C_1 = - \frac{3 \varepsilon_0}{\varepsilon_1 + 2 \varepsilon_0} E_0 \tag{11}\]から、求めたかった誘電体球による静電ポテンシャルは
\[\Phi_1 = - \frac{3 \varepsilon_0}{\varepsilon_1 + 2 \varepsilon_0} E_0 r \cos \theta, \quad \Phi_\mathrm{P} = \frac{\varepsilon_1 - \varepsilon_0}{\varepsilon_1 + 2 \varepsilon_0} \frac{a^3}{r^3} E_0 r \cos \theta \tag{12}\]となります。 ここから、誘電体球内部の電場は
\[\mathbf{E}_1 = - \frac{\partial \Phi_1}{\partial z} \mathbf{e}_z = \frac{3 \varepsilon_0}{\varepsilon_1 + 2 \varepsilon_0} E_0 \tag{13}\]と計算されます。 ここで\(\mathbf{e}_z\)は\(z\)軸方向の単位ベクトルです。
ここで一様電場中に置かれた誘電体球に誘起される電場を、電気双極子モーメントを用いてモデル化しましょう。 この電気双極子モーメントを\(\mathbf{d}\)とすると、これが十分遠方で作る静電ポテンシャルは
と書かれます。 この式と(12)式の\(\Phi_\mathrm{P}\)を見比べることで、この誘電体球の存在が、次の式で定義される電気双極子モーメントと等価であるとわかります。
\[\mathbf{d} = \frac{\varepsilon_1 - \varepsilon_0}{\varepsilon_1 + 2 \varepsilon_0} a^3 \mathbf{E}_0 \tag{15}\]
誘電体球による電磁波の散乱
静電場での議論を、電磁波の場合に拡張しましょう。 電場の変化を\(\mathbf{E} = \mathbf{E}_0 \cos (\omega t + \phi)\)のように考えますが、誘電体球の半径\(a\)が電磁波の波長に比べて十分小さいとします。 すると誘電体球内部に誘起される電気双極子モーメントは、これまで議論してきた一様な電場中の誘電体球の場合と同じと考えて差し支えないでしょう。 よって
\[\mathbf{d} (t) = \frac{\varepsilon_1 - \varepsilon_0}{\varepsilon_1 + 2 \varepsilon_0} a^3 \mathbf{E}_0 \cos (\omega t + \phi) \tag{16}\]となります。 この電気双極子モーメントの時間変化により発生する電磁放射の放射強度は、ラーモアの式で与えられます。
\[P_\mathrm{Larmor} = \frac{2e^2}{3c^3} \ddot{x}^2 = \frac{2}{3c^3} \ddot{d}^2 \qquad (\mathbf{d} = -e \mathbf{x}) \tag{17}\](16)式を代入すると
\[P = \frac{2}{3c^3} \omega^4 \left( \frac{\varepsilon_1 - \varepsilon_0}{\varepsilon_1 + 2 \varepsilon_0}\right)^2 a^6 E_0^2 \cos^2 (\omega t + \phi) \tag{18}\]この長時間平均を計算すると
\[\lim_{T \rightarrow \infty} \frac{1}{T} \int_0^T \cos^2 (\omega t + \phi) dt = \lim_{T \rightarrow \infty} \frac{1}{T} \int_0^T \frac{1 + \cos \{2(\omega t + \phi)\}}{2} dt = \frac{1}{2}\]より
\[\langle P \rangle = \frac{1}{3c^3} \omega^4 \left( \frac{\varepsilon_1 - \varepsilon_0}{\varepsilon_1 + 2 \varepsilon_0}\right)^2 a^6 E_0^2 \tag{19}\]のように計算されます。 入射電磁波のエネルギー流束の長時間平均は
\[\langle S \rangle = \frac{c}{8\pi} E_0^2 \tag{20}\]です。 これを用いると、散乱電磁波の放射強度の長時間平均が満たす式は、散乱断面積\(\sigma\)を用いて
\[\langle \frac{dP}{d\Omega} \rangle = \langle S \rangle \frac{d\sigma}{d\Omega} \ \Longrightarrow \ \langle P \rangle = \langle S \rangle \int_{4\pi} \frac{d\sigma}{d\Omega} d\Omega = \frac{c}{8\pi} E_0^2 \sigma \tag{21}\]のように書かれます。 (19)式を代入すると、散乱断面積は
\[\sigma (\omega) = \frac{8\pi}{3} \left( \frac{\varepsilon_1 - \varepsilon_0}{\varepsilon_1 + 2 \varepsilon_0}\right)^2 a^6 \left( \frac{\omega}{c} \right)^4 \propto \frac{a^6}{\lambda^4} \tag{22}\]のように求まります。 この式から、波長が短いほど散乱断面積が大きくなり、散乱されやすいことがわかります。
地球大気への応用: 青空と夕焼け
(22)式において、\(n \equiv \sqrt{\varepsilon_1 / \varepsilon_0}\)で定義される屈折率、そして\(\omega = \frac{2\pi c}{\lambda}\)を用いると
\[\sigma (\lambda) = \frac{128\pi^5}{3} \left( \frac{n^2 - 1}{n^2 + 2}\right)^2 \frac{a^6}{\lambda^4} \tag{23}\]のように書き直すことができます。 地球大気の成分固有の値である\(n, a\)を実験から測定すれば、ある波長\(\lambda\)に対する散乱断面積\(\sigma(\lambda)\)を計算することができます。
この散乱断面積を用いて、実際に太陽からの光がどの程度散乱されるかを計算する式を導出しましょう。 太陽から地球に垂直に光が降り注ぐことを考えます。 地表からの高度\(z\)での光の強度を\(I(z)\)、そして地球大気中の分子数密度は\(N(z) = N_0 e^{-z/\mu}\)のように、重力成層を成しているとします。 \(\mu\)は地球大気のスケールハイトです。 地球大気を形成する分子を誘電体球と見なし、(23)式の散乱断面積が適用できるとします。 上空から\(-dz\)進む間に、地表に向かう光線は\(N (-dz)\)個の分子と衝突をします。 このことから、光線の強度変化は\(dI = \sigma I Ndz\)です。 よって
を得ます。 ここで\(I_\infty\)は、\(z \rightarrow \infty\)での光の強度です。 この式から、地表\(z=0\)での光の強度は
\[I_0 = I_\infty e^{-\sigma \mu N_0} \tag{25}\]とわかります。 後は散乱断面積\(\sigma\)、地球大気における\(\mu, N_0\)を用いて\(I_0/I_\infty\)を計算すれば、その波長における光の強度の何割が地表に到達しているのかを算出することが可能です。 \(\sigma\)が大きいほど((47)式より波長が短いほど)散乱を強く受けます。 これが昼間の空全体が青く、夕焼けが赤い理由です。
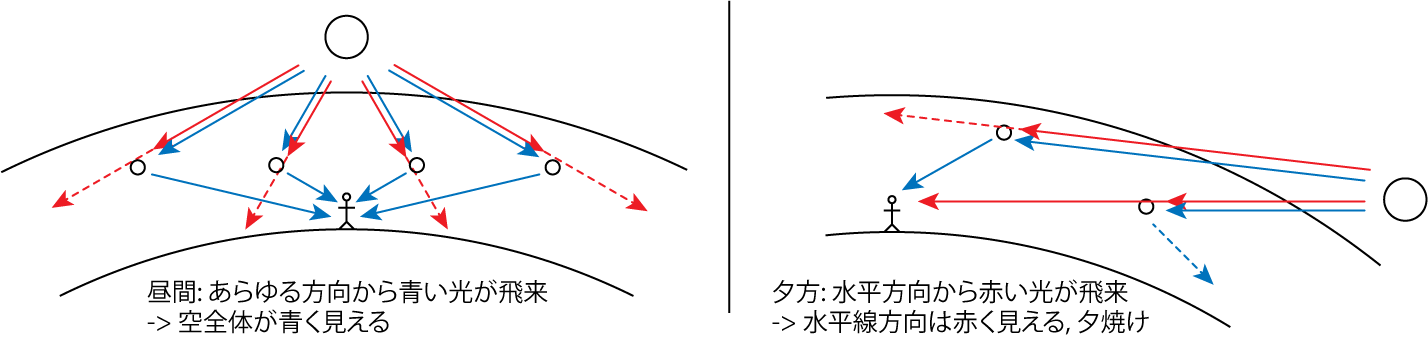
火星の夕焼けは青い
地球大気と異なる組成を持つ火星大気では、その光の散乱の様相も異なります。 火星地表から太陽の沈む様子を見ると、太陽の方向が青く輝いて見えることが、火星地表探査機から送られた画像により判明しました。 これは、火星での光の散乱は、地表から舞い上がった砂塵によるものであるためと考えられています。 砂塵粒子の大きさは地球大気に含まれる分子よりも大きいため、ここで議論されてきたようなレイリー散乱が適用できません。 冒頭で記述したように、より大きな粒子による電磁波の散乱過程であるミー散乱を用いた議論が必要です。 この砂塵の粒子の場合、赤い光がよく散乱されるため、日中は空が赤くなります。 そして日が沈み始めると、青い光がよく透過してくるために、夕焼けが青く見えます。
補遺: レイリー散乱のもう一つの導出法、束縛された電子による電磁波の散乱
束縛電子による電磁波の散乱について考えることで、レイリー散乱を導出することもできます。 これは先程の誘電体球に誘起される電機双極子モーメントを、周期的な運動をする電子であると見なすことから得られるものです。 ただし、電子が加速度運動することで放射を出す場合、厳密には以下のように放射を出すことによる反作用も考える必要があります。
放射による反作用
電子が何らかの束縛を受けて周期的な運動をしているとし
\[\mathbf{v} (t_1) = \mathbf{v} (t_2) = \mathbf{0} \tag{26}\]であるとします。 また、以下では電子の速度は非相対論的であるとします。 電子は加速度運動を受けて放射を出し、エネルギーを失います。 このエネルギーを失う効果を、「放射による反作用」と考え、放射が出る分だけ電子に減衰力がはたらくものと考えましょう。 すなわち、減衰力を\(\mathbf{f}\)とすると(\(t_1 \sim t_2\)の間に減衰力\(\mathbf{f}\)のする仕事)=(\(t_1 \sim t_2\)の間にラーマーの式で与えられる放射によるエネルギー損失量)のようにモデル化します。 これを式で改めて書き表すと
\[\int_{t_1}^{t_2} \mathbf{f} \cdot \mathbf{v} dt = - \int_{t_1}^{t_2} P_\mathrm{Larmor} dt = - \frac{2e^2}{3c^3} \int_{t_1}^{t_2} \dot{v}^2 dt \tag{27}\]のようになります。 ここで、最右辺の積分計算を進めましょう。
\[\int_{t_1}^{t_2} \dot{v}^2 dt = \int_{t_1}^{t_2} \dot{\mathbf{v}} \cdot \dot{\mathbf{v}} dt \underbrace{=}_{部分積分} \underbrace{\left[ \mathbf{v} \cdot \dot{\mathbf{v}} \right]_{t_1}^{t_2}}_{=0} - \int_{t_1}^{t_2} \mathbf{v} \cdot \ddot{\mathbf{v}} dt \tag{28}\](2), (3)式より
\[\int_{t_1}^{t_2} \mathbf{f} \cdot \mathbf{v} dt = \frac{2e^2}{3c^3} \int_{t_1}^{t_2} \mathbf{v} \cdot \ddot{\mathbf{v}} dt \tag{29}\]です。 両辺の形を見比べることで
\[\mathbf{f} = \frac{2e^2}{3c^3} \ddot{\mathbf{v}} \tag{30}\]とわかります。 今、電子が周期的な運動をしていると考えているため、\(\mathbf{v} \propto e^{-i\omega_0 t}\)であるとすれば
\[\mathbf{f} = - \frac{2e^2}{3c^3} \omega_0^2 \mathbf{v} = - m_e \tau \omega_0^2 \mathbf{v} \qquad \left( \tau \equiv \frac{2e^2}{3m_ec^3} \sim 10^{-23} \ [s] \right) \tag{31}\]のように求まります。
入射電磁波が存在する場合の、束縛電子の運動
質量\(m_e\)、電荷\(-e\)の電子が
\[\ddot{x} = - \omega_0^2 x -\omega_0^2 \tau \dot{x} \tag{32}\]に従って一次元運動をしているとします。 ここでも電子の運動は非相対論的極限で\(\dot{x} \ll c\)とし、さらに電子の角振動数は\(\omega_0 \tau \ll 1\)とします。 座標設定は電子の運動方向を\(x\)軸にとります。 入射電磁波は\(x\)方向に垂直な方向に進行し、\(x\)方向に直線偏光した角振動数\(\omega\)の電磁波とします。 すると、入射電磁波の電場は
\[E(t) = E_0 \cos \omega t \tag{33}\]のように書かれます。 この電磁波が入射してきた後の、電子の運動方程式は
\[\ddot{x} = - \omega_0^2 x -\omega_0^2 \tau \dot{x} - \frac{eE_0}{m_e} \cos \omega t \tag{34}\]となります。 この方程式の解は、\(\ddot{x} + \omega_0^2 \tau \dot{x} + \omega_0^2 x = 0\)の一般解と、\(\ddot{x} + \omega_0^2 \tau \dot{x} + \omega_0^2 x + \frac{eE_0}{m_e} \cos \omega t= 0\)の特解を足し合わせたものです。
- \(\ddot{x} + \omega_0^2 \tau \dot{x} + \omega_0^2 x = 0\)の一般解
\(x = e^{\lambda t}\)の形で求めてみましょう。
\[\lambda^2 + \omega_0^2 \tau \lambda + \omega_0^2 = 0 \ \Longrightarrow \ \lambda = \frac{-\omega_0^2 \tau \pm \sqrt{\omega_0^4 \tau^2 -4\omega_0^2}}{2} \tag{35}\]よって
\[x = e^{-\frac{\omega_0^2 \tau}{2} t} (C_1 e^{\frac{\sqrt{\omega_0^4 \tau^2 -4\omega_0^2}}{2}} + C_2 e^{-\frac{\sqrt{\omega_0^4 \tau^2 -4\omega_0^2}}{2}}) \tag{36}\]と求まります。 ここで\(C_1, C_2\)は初期条件から求まる定数です。
- \(\ddot{x} + \omega_0^2 \tau \dot{x} + \omega_0^2 x + \frac{eE_0}{m_e} \cos \omega t= 0\)の特解
\(x = C_3 \cos (\omega t + \phi)\)の形で求めてみましょう。
\[\begin{align} &-\omega^2 C \cos (\omega t + \phi) -\omega_0^2 \tau \omega C \sin (\omega t + \phi) + \omega_0^2 C \cos (\omega t + \phi) = - \frac{e E_0}{m_e} \cos \omega t \notag \\ &\Longrightarrow \ (\omega_0^2 - \omega^2) C (\cos \omega t \cos \phi - \sin \phi \sin \omega t) - \omega_0^2 \tau \omega C (\sin \omega t \cos \phi + \cos \omega t \sin \phi) = -\frac{eE_0}{m_e} \cos \omega t \notag \\ &\Longrightarrow \ C \{(\omega_0^2 - \omega^2) \cos \phi - \omega_0^2 \tau \omega \sin \phi \} \cos \omega t + C \{ -(\omega_0^2 - \omega^2) \sin \phi - \omega_0^2 \tau \omega \cos \phi \} \sin \omega t = -\frac{eE_0}{m_e} \cos \omega t \tag{37} \end{align}\]右辺と左辺を比較すると、\(\sin \omega t\)の係数から
\[(\omega^2 - \omega_0^2) \sin \phi - \omega_0^2 \tau \omega \cos \phi = 0 \ \Longrightarrow \ \tan \phi = \frac{\omega_0^2 \tau \omega}{\omega^2 - \omega_0^2} \tag{38}\]また、\(\cos \omega t\)の係数より
\[\begin{align} &C \cos \phi \{(\omega_0^2 - \omega^2) - \omega_0^2 \tau \omega \tan \phi \} = C \cos \phi (\omega^2 - \omega_0^2) \left( -1 - \frac{\omega_0^2 \tau \omega}{\omega^2 - \omega_0^2} \tan \phi \right) \notag \\ &\qquad \underbrace{=}_{(12)} - C \cos \phi (\omega^2 - \omega_0^2) \left( 1 + \tan^2 \phi \right) = - C \frac{\omega^2 - \omega_0^2}{\cos \phi} = - \frac{eE_0}{m_e} \notag \\ &\Longrightarrow \ C = \frac{eE_0}{m_e} \frac{\cos \phi}{\omega^2 - \omega_0^2} = \frac{eE_0}{m_e} \frac{1}{(\omega^2 - \omega_0^2) \sqrt{1+\tan^2 \phi}} \underbrace{=}_{(12)} \frac{eE_0}{m_e} \frac{1}{(\omega^2 - \omega_0^2) \sqrt{1+\left( \frac{\omega_0^2 \tau \omega}{\omega^2 - \omega_0^2}\right)}} \notag \\ &\qquad = \frac{eE_0}{m_e} \frac{1}{\sqrt{(\omega^2 - \omega_0^2)^2 + (\omega_0^2 \tau \omega)^2}} \tag{39} \end{align}\]求めたい(32)式の一般解は、これら2つを足し合わせたものです。 しかし、力学で減衰振動を勉強した方々であれば、\(\omega_0^2 \tau \dot{x}\)の項が減衰を表すものであることを知っているはずです。 この項により、周期的な運動をする粒子の振幅は減少していくと考えられますが、十分な時間が経過すると、減衰しきって系は定常状態に落ち着きます。 よって、ここでも十分時間が経過し、電子の運動が定常状態に落ち着いた場合の解を求めることにしましょう。 具体的には\(\omega_0^2 \tau t \gg 1\)のとき
\[x = \frac{eE_0}{m_e} \frac{1}{\sqrt{(\omega^2 - \omega_0^2)^2 + \Gamma^2 \omega^2}} \cos (\omega t + \phi) \qquad \left( \Gamma \equiv \omega_0^2 \tau, \quad \tan \phi = \frac{\Gamma \omega}{\omega^2 - \omega_0^2} \right) \tag{40}\]のような解となります。
電磁波の散乱と散乱断面積
散乱された電磁波を、入射電磁波により電子が運動することで起こった電磁放射であると考えます。 この問題では、電子の運動を非相対論的であると考えているため、この放射強度はラーモアの式で与えられます。
\[P_\mathrm{Larmor} = \frac{2e^2}{3c^3} \ddot{x}^2 \tag{41}\](40)式より
\[\ddot{x} = - \frac{eE_0}{m_e} \frac{\omega^2}{\sqrt{(\omega^2 - \omega_0^2)^2 + \Gamma^2 \omega^2}} \cos (\omega t + \phi) \tag{42}\]を代入すれば
\[P_\mathrm{Larmor} = \frac{2e^2}{3c^3} \frac{e^2 E_0^2}{m_e^2} \frac{\omega^4}{(\omega^2 - \omega_0^2)^2 + \Gamma^2 \omega^2} \cos^2 (\omega t + \phi) \tag{43}\]この長時間平均は
\[\lim_{T \rightarrow \infty} \frac{1}{T} \int_0^T \cos^2 (\omega t + \phi) dt = \lim_{T \rightarrow \infty} \frac{1}{T} \int_0^T \frac{1 + \cos \{2(\omega t + \phi)\}}{2} dt = \frac{1}{2}\]より
\[\langle P_\mathrm{Larmor} \rangle = \frac{e^4 E_0^2}{3m_e^2 c^3} \frac{\omega^4}{(\omega^2 - \omega_0^2)^2 + \Gamma \omega^2} \tag{44}\]のように計算されます。
入射電磁波のエネルギー流束の長時間平均は
です。 これを用いると、散乱電磁波の放射強度の長時間平均は
\[\langle \frac{dP_\mathrm{Larmor}}{d\Omega} \rangle = \langle S \rangle \frac{d\sigma}{d\Omega} \ \Longrightarrow \ \langle P_\mathrm{Larmor} \rangle = \langle S \rangle \int_{4\pi} \frac{d\sigma}{d\Omega} d\Omega = \frac{c}{8\pi} E_0^2 \sigma \tag{46}\]のように書かれます。 ここで\(\sigma\)は散乱断面積です。 (44)式を代入すると
\[\sigma (\omega) = \frac{8\pi}{3} \left( \frac{e^2}{m_e c^2}\right)^2 \frac{\omega^4}{(\omega^2 - \omega_0^2)^2 + \Gamma^2 \omega^2} = \frac{\omega^4}{(\omega^2 - \omega_0^2)^2 + \Gamma^2 \omega^2} \sigma_\mathrm{T} \tag{47}\]となります。 ここで、\(\sigma_\mathrm{T} = \frac{8\pi}{3} \left( \frac{e^2}{m_e c^2}\right)^2\)はトムソン散乱断面積です。
\(\omega \gg \omega_0\)の場合
この\(\sigma (\omega)\)は、\(\omega \gg \omega_0\)の極限では
\[\sigma (\omega) = \frac{\sigma_\mathrm{T}}{\left(1 - \frac{\omega_0^2}{\omega^2}\right)^2 + \frac{\Gamma^2}{\omega^2}} \simeq \sigma_\mathrm{T} \tag{48}\]のように、トムソン散乱断面積に一致します。 入射電磁波の角振動数よりも電子の周期運動の角振動数が十分小さい場合、入射電磁波にとっては電子は静止しているように見えます。 これは、自由電子による散乱現象に一致するため、散乱断面積はトムソン散乱のものと一致すると解釈することができます。
\(\omega \simeq \omega_0\)の場合
(47)式より
\[\begin{align} \sigma (\omega) &= \frac{\omega^4}{(\omega - \omega_0)^2 (\omega + \omega_0)^2 + \Gamma^2 \omega^2} \sigma_\mathrm{T} \simeq \frac{\omega_0^4}{4\omega_0^2 (\omega - \omega_0)^2 + \Gamma^2 \omega_0^2} \sigma_\mathrm{T} \notag \\ &\underbrace{=}_{(6)} \frac{4\pi e^2}{m_e c} \frac{\tau \omega_0^2}{4 (\omega - \omega_0)^2 + \Gamma^2} = \frac{2\pi^2 e^2}{m_e c} \frac{\Gamma / (2\pi)}{(\omega - \omega_0)^2 + (\Gamma / 2)^2} \tag{49} \end{align}\]となります。 これを共鳴散乱(resonance scattering)の断面積と呼びます。 (49)式の形はローレンツ型の分布と呼ばれる有名な関数形です。 これを\(\omega\)で積分すると
\[\int_0^\infty \frac{\Gamma / (2\pi)}{(\omega - \omega_0)^2 + (\Gamma / 2)^2} d\omega \underbrace{=}_{\omega - \omega_0 = \frac{\Gamma}{2} \tan \theta} \frac{\Gamma}{2} \int_0^{\pi / 2} \frac{1}{(\Gamma / 2)^2} \frac{\Gamma / 2}{\cos^2 \theta} \frac{d\theta}{1 + \tan^2 \theta} = \frac{1}{2}\]より
\[\int_0^\infty \sigma (\omega) d\omega = \frac{\pi^2 e^2}{m_e c} \tag{50}\]と求まります。
\(\omega \ll \omega_0\)の場合
\[\sigma (\omega) \underbrace{=}_{\Gamma = \omega_0^2 \tau} \frac{\omega^4}{\omega_0^4} \frac{\sigma_\mathrm{T}}{\left( \frac{\omega^2}{\omega_0^2} - 1\right)^2 + \tau \frac{\omega^2}{\omega_0^2}} \simeq \frac{\omega^4}{\omega_0^4} \sigma_\mathrm{T} \propto \omega^4 \tag{51}\]のように近似されます。 (51)式から、短波長になるほどより散乱断面積が大きくなり、散乱されやすくなるとわかります。
\(\sigma (\omega)\)の図示
最後に、(47)式で表現される散乱断面積を図示しましょう。
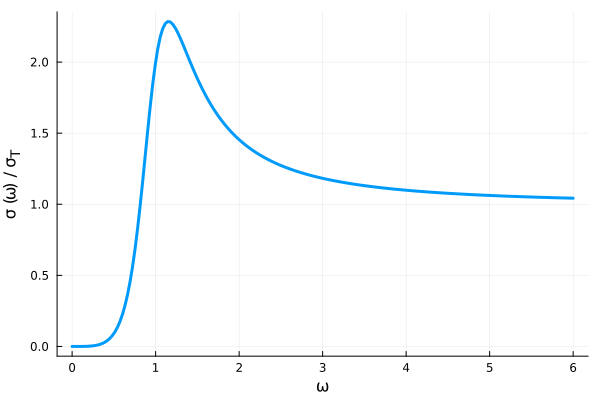
この図では、\(\Gamma = 0.5\)、また縦軸は\(\sigma(\omega) / \sigma_\mathrm{T}\)、横軸は\(\omega / \omega_0\)のように規格化しています。 \(\omega / \omega_0\)が小さいところでは4乗に比例して大きくなります。 \(\omega / \omega_0 \sim 1\)ではローレンツプロファイルのようになり、\(\omega / \omega_0 \gg 1\)では\(\sigma / \sigma_\mathrm{T} \rightarrow 1\)に漸近しています。
参考文献
[1] 中村哲, 須藤彰三, “電磁気学”
[2] ランダウ & リフシッツ, “場の古典論”
[3] 砂川重信, “理論電磁気学”
[4] 太田浩一, “電磁気学の基礎I”
[5] 太田浩一, “電磁気学の基礎II”
[6] 後藤憲一, 山﨑修一郎, , “詳解電磁気学演習”
[7] 平川浩正, “電気力学”
[8] 中村文隆, 鶴剛, 長田哲也, 藤沢健太, 梅村雅之, 福江純, “放射素過程の基礎”
[9] NASA Solar System Exploration, “What Does a Sunrise-Sunset Look Like on Mars?”