Table of contents
Amplify
Amplifyとは
概要
フィックスターズが開発・提供している、イジングマシンに対応したアプリケーション開発を支援するSDKです。Pythonを用いて組合せ最適化を定式化し、ソルバーを用いて最適化計算を行うことができます。
対応ハードウェア
2021年2月現在、以下のハードウェアに対応しています。
- D-Wave Systems: 2000Q/Advantage
- 富士通: デジタルアニーラ
- 東芝: Simulated Bifurcation Machine
- 日立: CMOSアニーリングマシン
- フィックスターズ: Amplify Annealing Engine
Amplifyウェブサイトにマシン性能の比較早見表があります。詳しくは以下をご覧ください。
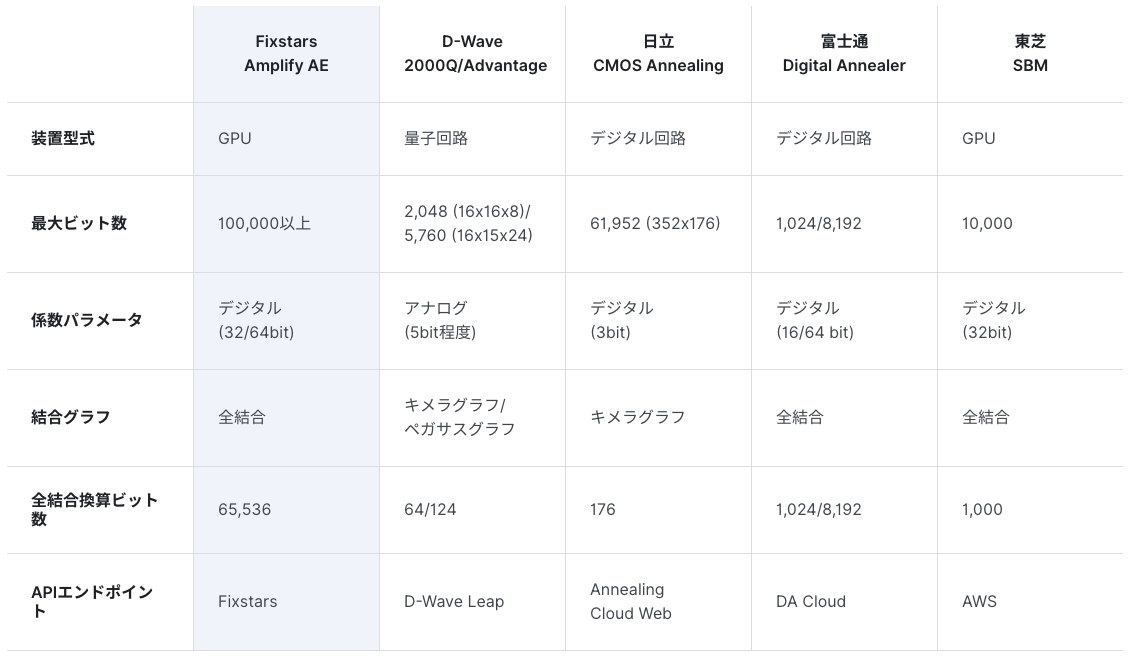
料金プラン
Amplifyの料金プランの詳細を以下に示します(2021年2月現在)。
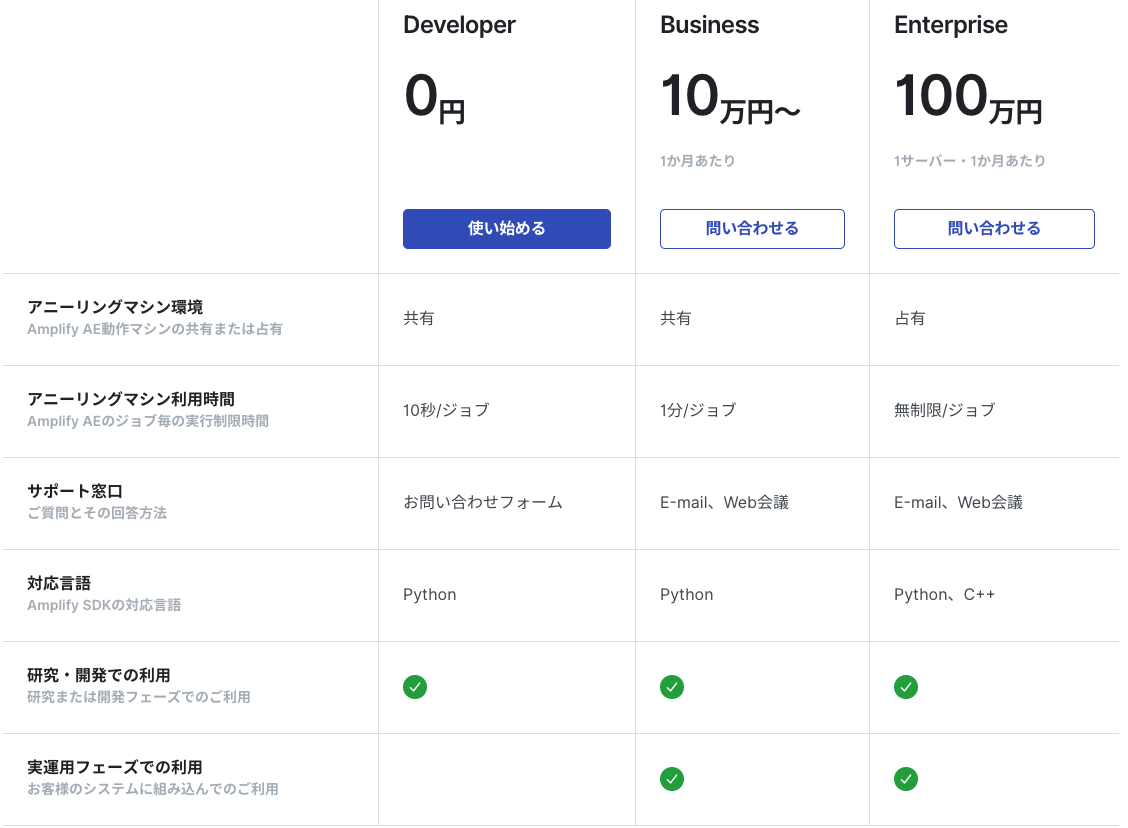
筆者は(お金がないため)ひとまずDeveloperプランを利用しています。このプランで使えるのは、Amplify Annealing Engineを1回の計算につき10秒までとなっています。
Python SDKの使用感
ここでは実際にAmplifyを使ってQUBO定式化されたものを実装したときに感じた長所・短所を記述します。例としてTSPを実装しました。
モデル構築
以下にモデル構築部分のPythonスクリプトを示します。
from amplify import BinaryPoly, gen_symbols, sum_poly from amplify.constraint import equal_to
def make_hamiltonian(d, feed_dict):
# set the number of cities
N = len(d)
# set hyperparameters
lambda_1 = feed_dict['h1']
lambda_2 = feed_dict['h2']
# make variables
x = gen_symbols(BinaryPoly, N, N)
# set One-hot constraint for time
h1 = [equal_to(sum_poly([x[n][i] for n in range(N)]), 1) for i in range(N)]
# set One-hot constraint for city
h2 = [equal_to(sum_poly([x[n][i] for i in range(N)]), 1) for n in range(N)]
# compute the total of constraints
const = lambda_1 * sum(h1) + lambda_2 * sum(h2)
# set objective function
obj = sum_poly(N, lambda n: sum_poly(N, lambda i: sum_poly(N, lambda j: d[i][j]*x[n][i]*x[(n+1)%N][j])))
# compute model
model = obj + const
return x, model
gen_symbols()
変数配列を生成します。第一引数にBinaryPolyを指定するとバイナリ多項式を表現するためのバイナリ変数を、IsingPolyを指定するとスピン変数による多項式を表現するためのスピン変数を生成することができます。
equal_to()
equal_toで等式制約を実装することができます。例えば
h1 = [equal_to(sum_poly([x[n][i] for n in range(N)]), 1) for i in range(N)]
は以下の実装を行ったことと等価です。
\[\sum_{n} x_{ni} = 1 \quad (\forall i)\]その他、Amplifyではless_equal(), greater_equal(), clamp()で不等式制約を簡単に表現することができます。
sum_poly()
sum_poly(N, f(n))は\(\sum_{n=0}^{N-1} f(n)\)を表す関数です。
obj = sum_poly(N, lambda n: sum_poly(N, lambda i: sum_poly(N, lambda j: d[i][j]*x[n][i]*x[(n+1)%N][j])))
のようにlambda式を使ってf(n)部分を表現しています。
計算実行
イジングマシンのクライアントを作成しパラメータを設定、そしてソルバーを作成しクライアントを設定することでモデル構築の部分で実装した問題を解くことができます。
from amplify import Solver
from amplify.client import FixstarsClient
def solve_problem(model):
# set client and parameters
client = FixstarsClient()
client.token = "xxxxxxxxxxxxxxxxxxxx"
client.parameters.timeout = 5000
# set solver
solver = Solver(client)
# get result
result = solver.solve(model)
# extract value of objective function and binary variables
obj, values = result[0].energy, result[0].values
# get values of constraints
broken = model.check_constraints(values)
return obj, values, broken
client
クライアントにはFixstarsClient, DWaveClient, DWaveSamplerClient, LeapHybridSamplerClientなどを選択することができます。
solver
soverメソッドにモデルを入力することで、指定されたclient上で計算が実行されます。
result
resultには制約を満たした解のリストが格納されています。もし制約を満たす解が得られなかった場合には、空のリストが返されます。実行可能解以外をフィルタする機能は、ソルバークラスのfilter_solutionをFalseにすることで無効化できます。energyでコスト関数(目的関数)の値を、valuesで入力変数の値を辞書で取得できます。
check_constraints
この関数の引数にvaluesを用いることで、その解がどの制約を満たしているか/どの制約を満たしていないかを確認することができます。実際の出力を以下に示します。
[((q_0 + q_5 + q_10 + q_15 + q_20 == 1.000000, 1), True), ((q_1 + q_6 + q_11 + q_16 + q_21 == 1.000000, 1), True), ((q_2 + q_7 + q_12 + q_17 + q_22 == 1.000000, 1), True), ((q_3 + q_8 + q_13 + q_18 + q_23 == 1.000000, 1), True), ((q_4 + q_9 + q_14 + q_19 + q_24 == 1.000000, 1), True), ((q_0 + q_1 + q_2 + q_3 + q_4 == 1.000000, 1), True), ((q_5 + q_6 + q_7 + q_8 + q_9 == 1.000000, 1), True), ((q_10 + q_11 + q_12 + q_13 + q_14 == 1.000000, 1), True), ((q_15 + q_16 + q_17 + q_18 + q_19 == 1.000000, 1), True), ((q_20 + q_21 + q_22 + q_23 + q_24 == 1.000000, 1), True)]
Trueは制約が満たされているもの、Falseは制約が満たされていないものを表します。
解の解析
上述までに得られたvaluesは入力変数と解の値のマッピングを表す辞書です。このままでは評価しづらいので、これをデコードします。Amplifyにもこの機能が備わっています。
x_sol = decode_solution(x, values)
使用してみた感想(長所・短所含む)
- PyQUBOと同じかそれ以上に簡単に最適化問題の実装ができる
- 不等式制約も簡単に実装できそう
- LogEncIntegerなど無い機能もある(まだ私が見つけていないだけかもしれない、要チェック)
- 複雑な制約・目的関数(例えば和を計算するときの添字について\(i>j, i\neq 0\)などがある場合)は記述が冗長になりそう?
- どの制約が破れているのか見にくい(制約1つずつにラベルを割り当てることはできない?)
参考資料
- [1] Amplify website
- [2] Amplify document