Table of contents
冷たい等方プラズマ中の電磁波の伝播
ここでは、(熱運動が無視できるような)冷たい一様等方プラズマ中の電磁波の伝播について考察していきましょう。 宇宙空間のプラズマはほとんどの場合、近接する粒子間のクーロンポテンシャルに比べて、粒子の運動エネルギーの方が圧倒的に大きい状態、すなわち弱結合プラズマ状態にあります。 任意の電磁波は、2つの直交する直線偏光に分解することができます。 そこで以下では、一つの方向に直線偏光した電磁波の伝播を考えていきましょう。 系には特徴的な方向が存在しないため、任意の電磁波の伝播は、この結果を重ね合わせることで表現できます。
方程式の線形化
電子とイオンの数密度は至る場所で\(n\)で等しくなっており、電気的中性が常に成り立っているものとします。 さらにイオンは電子に比べて非常に重いため、常に静止していると考えて良いものとします。
このようなプラズマ中を電磁波が伝播する様子を調べましょう。 電磁波が入射する前では、電場・磁場・電子の速度・電流・電荷密度はすべてゼロであるとします。 これらは電磁波が入射したことにより発生する摂動量としてのみ有限値を取ります。 このことから、マクスウェル方程式そして電子の運動方程式を摂動量の一次まで展開し、線形化して解いていきます。 線形方程式の解は、一次独立な固有解の重ね合わせで表現できます。 よって、一つのフーリエモードを取り出してその性質を調べていけば、線形方程式の解の振る舞いを調べることとしては十分でしょう。 すなわち
のような形として方程式を解いていきます。
マクスウェル方程式
\[\nabla \cdot \mathbf{E} = 4\pi \rho \underbrace{=}_{電気的中性条件より} 0\tag{2}\] \[\nabla \cdot \mathbf{B} = 0 \tag{3}\] \[\nabla \times \mathbf{E} = - \frac{1}{c} \frac{\partial \mathbf{B}}{\partial t} \tag{4}\] \[\nabla \times \mathbf{B} = \frac{4\pi}{c} \mathbf{j} + \frac{1}{c} \frac{\partial \mathbf{E}}{\partial t} \tag{5}\]です。 ここで電子が運動をすることで発生する電流密度は
\[\mathbf{j} = -en\mathbf{v} \tag{6}\]と書かれます。 (1)式より、マクスウェル方程式はそれぞれ
\[\nabla \cdot \mathbf{E} = i \mathbf{k} \cdot \mathbf{E}, \quad \nabla \times \mathbf{E} = i \mathbf{k} \times \mathbf{E}, \quad \frac{\partial \mathbf{E}}{\partial t} = -i\omega \mathbf{E} \tag{7}\]などより
\[i \mathbf{k} \cdot \mathbf{E} = 0 \tag{8}\] \[i \mathbf{k} \cdot \mathbf{B} = 0 \tag{9}\] \[i \mathbf{k} \times \mathbf{E} = \frac{i\omega}{c} \mathbf{B} \tag{10}\] \[i \mathbf{k} \times \mathbf{B} = - \frac{4\pi en}{c} \mathbf{v} - \frac{i\omega}{c} \mathbf{E} \tag{11}\]となります。
電子の運動方程式
次に電子の運動方程式を考えましょう。 電磁波の入射により発生する電子の運動は非相対論的であるとして、ローレンツ力を無視すると、電子の運動方程式から
\[m_e \frac{d\mathbf{v}}{dt} = - e\mathbf{E} \ \Longrightarrow \ -im_e\omega \mathbf{v} = -e \mathbf{E} \ \Longrightarrow \ \mathbf{v} = \frac{e}{im_e \omega} \mathbf{E} \tag{12}\]を得ます。
分散関係式の導出
ここまで得られた結果を用いて\(\mathbf{B}, \mathbf{v}\)を消去し、一つの式にまとめましょう。 (11), (12)式より
\[i \mathbf{k} \times \mathbf{B} = i \frac{4\pi e^2 n}{m_e} \frac{1}{c \omega} \mathbf{E} - \frac{i\omega}{c} \mathbf{E} = i \left( \frac{\omega_\mathrm{pe}^2}{c \omega} - \frac{\omega}{c} \right) \mathbf{E}\tag{13}\]途中
\[\omega_\mathrm{pe} \equiv \sqrt{\frac{4\pi e^2 n}{m_e}} = \sqrt{\frac{4\pi}{m_e c^2} \frac{e^2}{\hbar c} \hbar c c^2} n_e^{1/2} \simeq \sqrt{\frac{12}{0.5} \frac{1}{140} 200 \times 10^{-13} \times (3 \times 10^{10})^2 } n_e^{1/2} \simeq 6 \times 10^4 n_e^{1/2} \tag{14}\]を定義しました。 これは電子プラズマ振動数と呼ばれるもので、電磁波の入射により生じた電荷分布の偏りから発生した電場を復元力とする振動の振動数です。 \(\omega_\mathrm{pe}\)は、入射してきた電磁波の振動数には依存せず、プラズマの電子数密度のみに依存することが特徴です。 さらに(10)式より
\[\mathbf{B} = \frac{c}{\omega} \mathbf{k} \times \mathbf{E} \tag{15}\](15)式より、(13)式の左辺は
\[\frac{ic}{\omega} \mathbf{k} \times (\mathbf{k} \times \mathbf{E}) = \frac{ic}{\omega} \{ \underbrace{(\mathbf{k} \cdot \mathbf{E})}_{(8)} \mathbf{k} - (\mathbf{k} \cdot \mathbf{k}) \mathbf{E} \} = - \frac{ick^2}{\omega} \mathbf{E} \tag{16}\]となります。 以上から
\[\left( \frac{c}{\omega} k^2 + \frac{\omega_\mathrm{pe}^2}{c\omega} - \frac{\omega}{c} \right) \mathbf{E} = \mathbf{0} \tag{17}\]\(\mathbf{E} \neq \mathbf{0}\)より、(17)式が恒等的に成り立つには
\[\frac{c}{\omega} k^2 + \frac{\omega_\mathrm{pe}^2}{c\omega} - \frac{\omega}{c} = 0 \ \Longrightarrow \ \omega^2 = \omega_\mathrm{pe}^2 + c^2 k^2 \tag{18}\]である必要があります。 このようにしてプラズマ中を伝播する電磁波の分散関係式を得ることができました。
伝播する電磁波の位相速度と進入長
(18)式から、この系を伝播する電磁波の位相速度を求めてみましょう。
\[k^2 = \frac{\omega^2 - \omega_\mathrm{pe}^2}{c^2} = \frac{\omega^2}{c^2} \left\{ 1 - \left(\frac{\omega_\mathrm{pe}}{\omega} \right)^2 \right\} \tag{19}\]より
\[v_p = \frac{\omega}{k} = \frac{c}{\sqrt{1 - \left(\frac{\omega_\mathrm{pe}}{\omega} \right)^2}} = \frac{c}{n} \tag{20}\](20)式より、プラズマは屈折率\(n = \sqrt{ 1 - \left(\frac{\omega_\mathrm{pe}}{\omega} \right)^2 }\)の媒質と見ることができます。 この屈折率の表記から、プラズマは屈折率が常に1以下で、位相速度は光速度を超える媒質です。
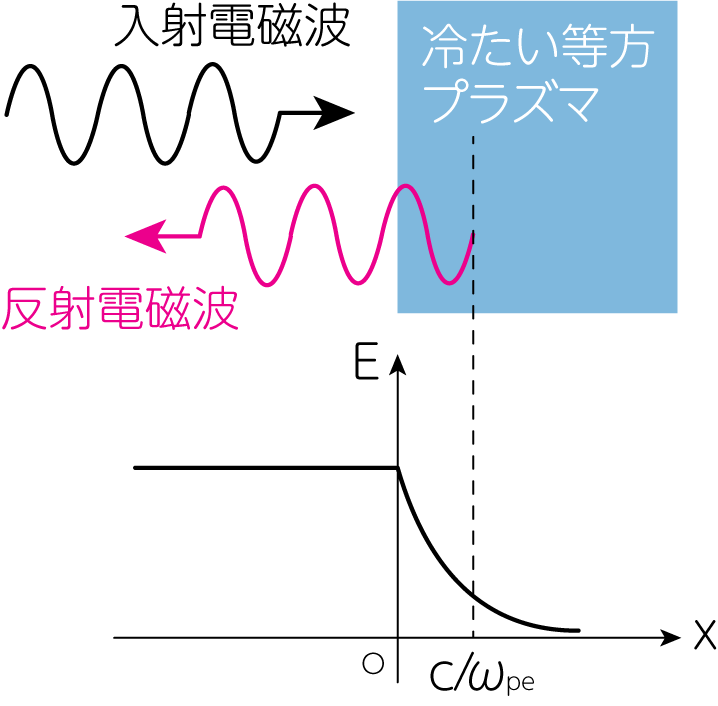
\(\omega < \omega_\mathrm{pe}\)の低周波数の場合、\(k\)が虚数になります。 つまりこのような低周波電磁波はプラズマ中を伝播することができず、外部からプラズマに入射する場合には、表面で反射されることになります。 \(\omega \ll \omega_\mathrm{pe}\)のときには
から、電磁波は表面から\(c/\omega_\mathrm{pe}\)程度の深さだけ進入して反射されます。 この\(c/\omega_\mathrm{pe}\)を進入長(penetration length)と呼びます。 先程のプラズマ振動数\(\omega_\mathrm{pe}\)が電磁波の振動数に依存しないことからわかるように、プラズマは摂動を与えると固有のプラズマ振動数で振動します。 それよりゆっくり振動することはできず、プラズマ振動数以下の振動数の電磁波はプラズマ中を伝播することができないことを示しています。
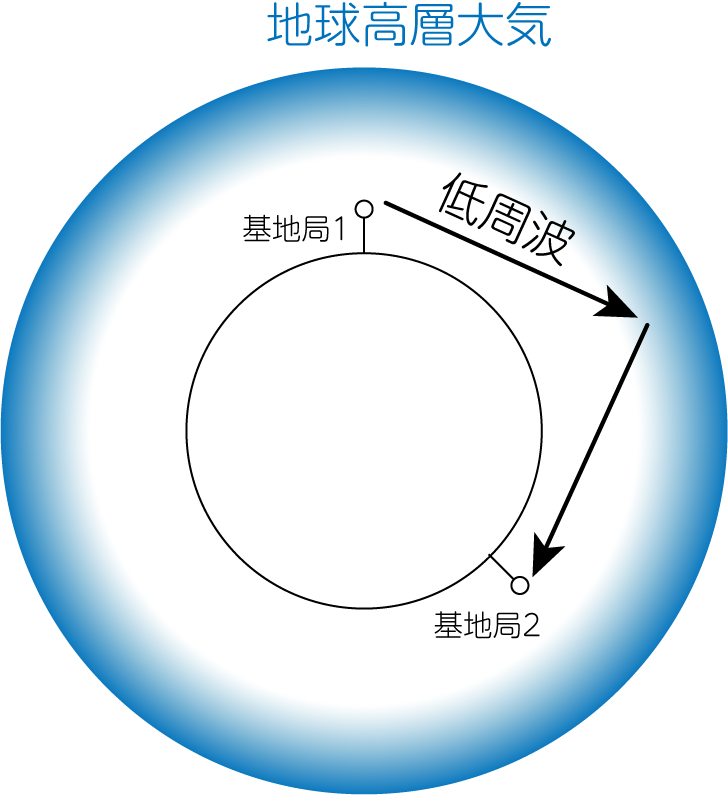
例えば、地球高層大気に存在する電離層の電子数密度\(n = 10^5 \mathrm{cm}^{-3}\)を代入すると、プラズマ振動数\(\nu_\mathrm{pe} = \omega_\mathrm{pe}/2\pi\)は3MHz程度になります。 したがって、3MHz以下の低周波電磁波を宇宙に向けて放射すると、電離層の表面で反射されます。 地球の裏側との交信に、この物理現象を利用していたこともあります。
プラズマの屈折率を利用した観測
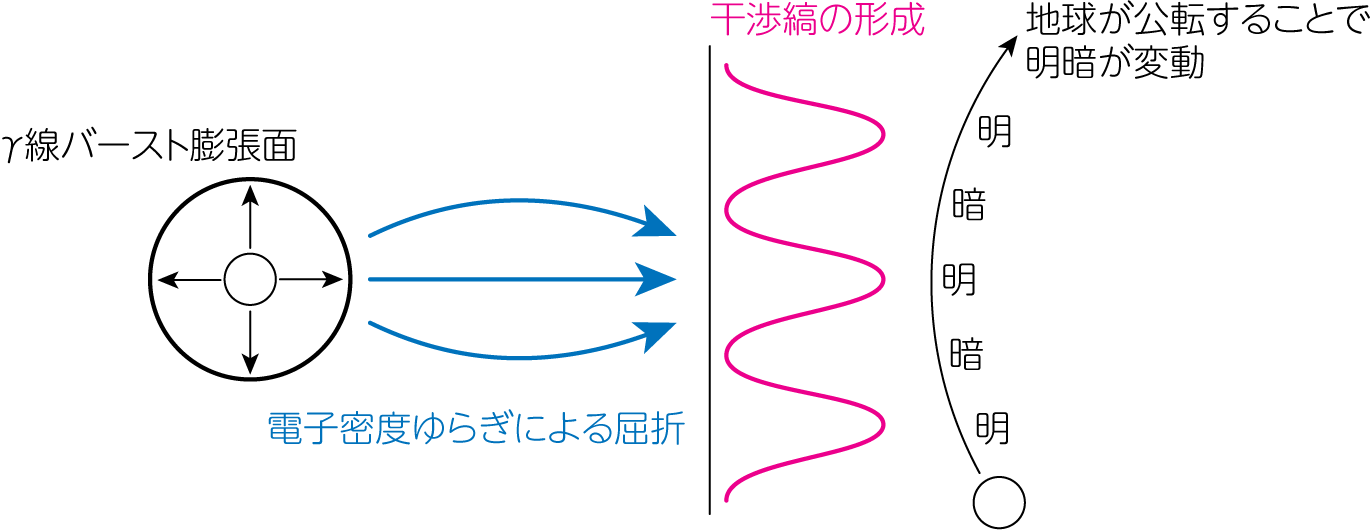
星間物質の電子数密度のゆらぎにより、伝播する電磁波の屈折角にもゆらぎが生じます。 天体の大きさが非常に小さい(点源)ときは、天体から異なる方向に放出された光線が観測者の位置で再び交差し、干渉縞を形成します。 この干渉縞中を地球の公転運動などにより地球が運動することで、天体の見かけの明るさが明るくなったり弱くなったり見えることがあります。 この現象をシンチレーション(scintillation, きらめきの意味)と呼びます。 この現象は非常に小さな天体の大きさを制限する方法として有効です。 例えば、γ線バーストの膨張速度を求めた研究があります。 γ線バースト源となる天体が爆発を起こし膨張を始めた頃は、先程の議論から明暗の干渉縞が見られます。 しかし膨張して大きくなると干渉効果が弱くなります。 干渉縞が見えなくなるまでの時間を計測すれば、おおよその膨張速度を求めることが可能です。
プラズマ中では位相速度が光速度を超える…相対論と矛盾している?
(19)式より\(\omega \rightarrow \omega_\mathrm{pe}\)となると、\(k \rightarrow 0\)に近づくことがわかります。 すると(20)式から\(v_p \rightarrow \infty\)となり、位相速度は光速度を越え、無限大に到達することができるように見えます。 これは相対論の光速度不変の原理を破っているのでしょうか。 実はこの話には、次のようなからくりが存在します。 簡単のため、プラズマでの振動ではなく、バネに繋がれた連制振り子を考えましょう。 この連制振り子の質点は全て同じ質量、振り子の長さも全て同じで、さらに振り子どうしを連結しているバネのバネ定数も全て同じであるとします。 この連制振り子では下図のように、全ての質点が同じタイミングで左右に振動することが許されます。
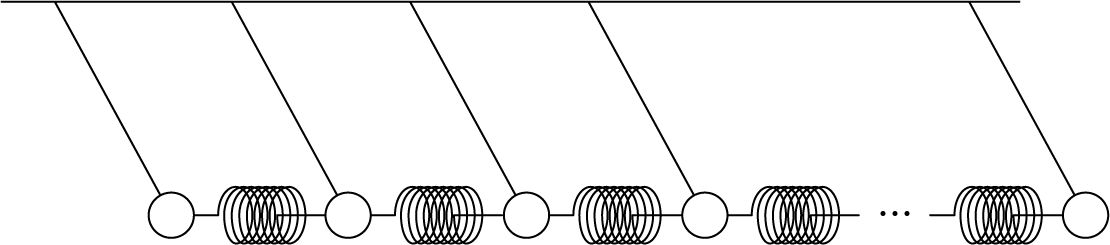
これらは全てが同位相に揃っています。 しかしこれは初期に誰かが同じ位相の状態を作り上げ、そこから手を離して左右にゆれるのを見ている状態であり、位相が無限大の速度で端から端まで伝搬しているのではありません。 位相速度は情報を伝えるものではない、ということを理解しておきましょう。
参考文献
[1] Goodman, 1997, “Radio scintillation of gamma-ray-burst afterglows”