Table of contents
高光度青色変光星 (Luminous Blue Variables: LBV)
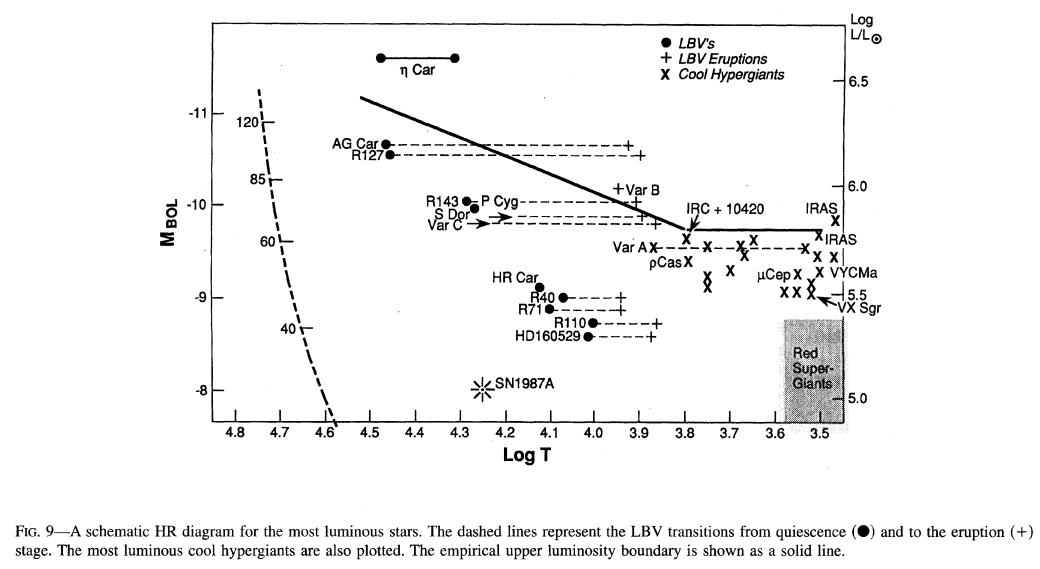
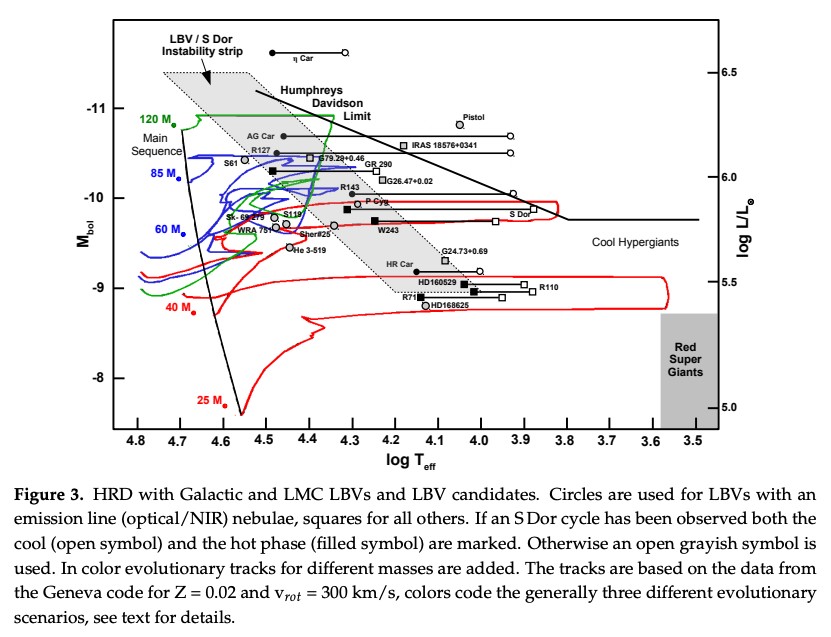
LBVの主な特徴は、光度が非常に大きく、種々の時間スケールで変光を示すことです。 それらの変光の原因は、今なお明らかになっていません。 その光度は\(-11 < M_\mathrm{bol} < -9 \ (5.5 < \log L/L_\odot < 6.5)\)で、それを質量に換算すると\(M \sim 50 M_\odot -120 M_\odot\)に対応します。 最も明るい恒星のグループであり、HR図上のハンフリー・デイヴィッドソン限界 (下図の実線)の近くに存在します。
LBVの変種
LBVには、種々の変種が存在します。
Major brightenning (eruption)
その変光幅は\(\Delta V \gtrsim 3 \mathrm{mag}\)であり、大きな質量放出を伴います。 そのような大きな増光が、\(\eta\) Carでは1837年に、そしてP Cygでは1600年に起こったことが知られています。
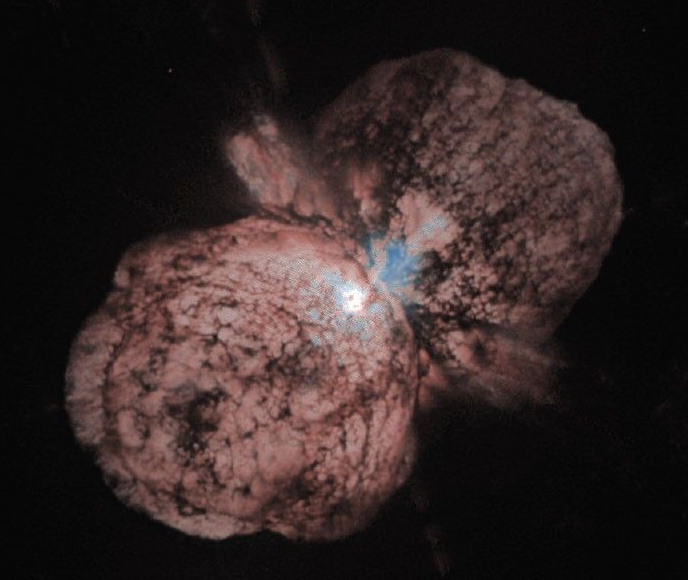
\(\eta\) Carはカリーナ星雲中の散開星団 Trumpler 16の一員で、2023年には約6等の星として観測されています。 見かけの明るさは明るくありませんが、距離が約2.5kpcもあるので非常に高い光度を持つことが予想され、その質量は約100\(M_\odot\)と推定されています。 \(\eta\) Carは1837年から約20年間、1等から0等の星として観測されたことが知られています。 この20年の間だけ、現在の100倍程度明るくなっていたことになります。 その間に大きな質量放出が起こり、それは現在2つのボールを並べたようなhomunculus nebula (人形星雲?)として観測されています。 なぜ20年間も続く爆発が起き、大きな質量放出が起こり、現在のような星雲の形になったのかは、未だ判明していません。
最近、\(\eta\) CarからのX線強度が5.5年の周期性を持つことが判明し、5.5年周期の連星系をなしていることがわかりました。 そのモデルによると、主星よりもコンパクトで高温の伴星が楕円率の大きい軌道上を回っており、X線は伴星からの恒星風と主星からの恒星風の衝突により放射されているとわかりました。 このモデルは、近点付近での満ち欠けによりX線強度が急激に落ちることを予想しました。 その予想通りに2003年6月末にX線強度が急激に減少し、この連星モデルがほぼ確かめられました。
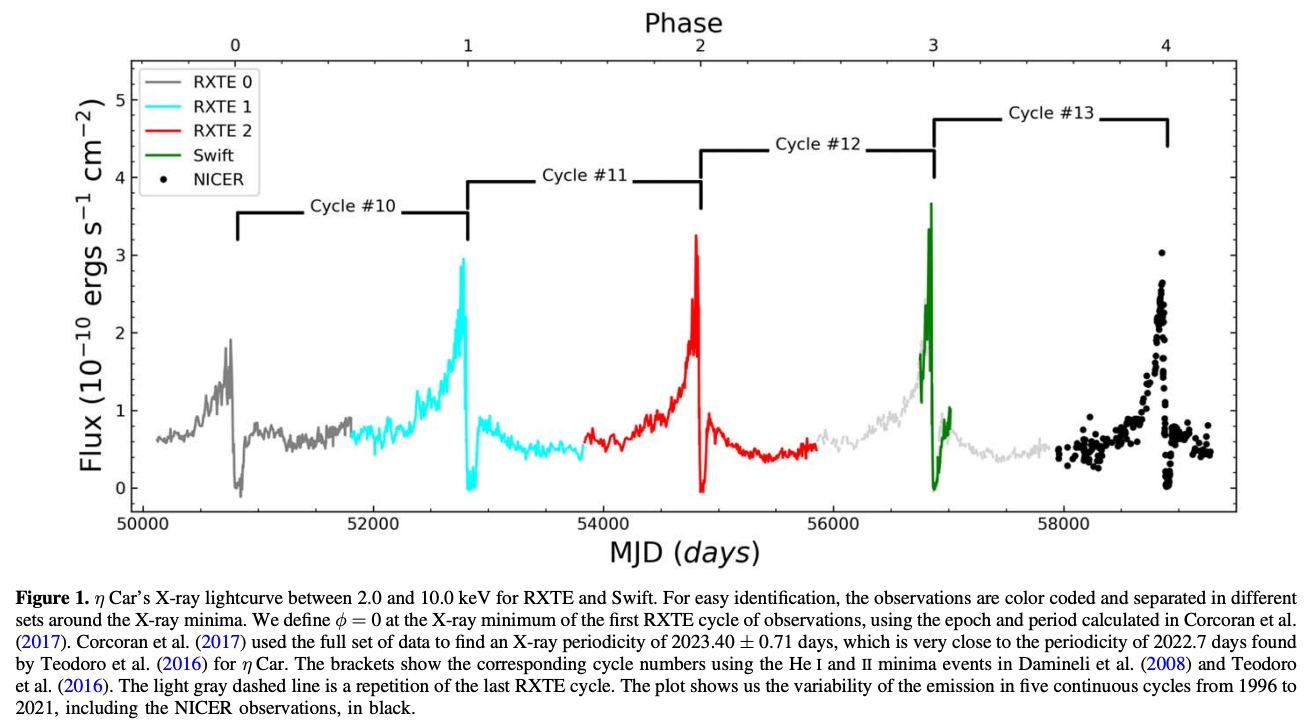
Esinoza-Galeas et al. (2022)より
しかし、連星系をなしていることが\(\eta\) Carの進化にどのような影響を及ぼしたのかは、明らかになっていません。
Moderate variations
LBVの典型的な変光で、その変更幅は\(0.5 \mathrm{mag} < \Delta V < 2.0 \mathrm{mag}\)ですが、ボロメトリック光度は一定であることが知られています。 したがって、\(V\)での変光は表面温度 (半径)の変化に伴う、ボロメトリック補正の変化によって生じています。 この変光の時間スケールは数年 (AG Car)から数十年(S Dor)に渡ります。
Photometric micro-variations
変光幅が\(\Delta V \lesssim 0.2 \mathrm{mag}\)とこれまでに比べて小さく、変光の時間スケールが数週間から数ヶ月と短いものです。 この種の変光は通常の超巨星にも見られ、非動径脈動ではないかと考えられています。
大きな質量損失率
LBVが速い質量放出をしていることは、それらのスペクトルがP Cygniプロファイルを示すことからわかっています。 質量放出率は最大光度 (最大半径)のときに最も大きく、その値は \(\dot{M} \sim 10^{-5} - 10^{-4} M_\odot / \mathrm{yr}\)となっています。
補遺: ハンフリーズ・デイヴィッドソン限界 (Humphreys-Davidson limit)
この限界は、Humphreys & Davidson (1979)で初めて示されました。 天の川銀河と大マゼラン雲中に存在する大質量星の観測データをHR図中にプロットしたところ、ある明るさ以上の恒星が存在しないことを経験的に示したのです。
明るさ・光度の上限と聞いて思い出すのはエディントン光度です。
\[L_\mathrm{edd} = \frac{4\pi c GM}{\kappa_\mathrm{el}} \tag{1}\]高温の恒星であるため、電子散乱による不透明度\(\kappa_\mathrm{el} = 0.2 (1+X)\)を用いましょう。 また大質量星内部の圧力が理想気体で記述できる場合、\(L \propto M^3\)となるため
\[\frac{4\pi c GM_\mathrm{max}}{\kappa_\mathrm{el}} \simeq M_\mathrm{max}^3 \ \Longrightarrow \ M_\mathrm{max} \simeq \sqrt{\frac{4\pi c G}{\kappa_\mathrm{el}}} M \tag{2}\]今、太陽と同じ組成の恒星を見ていると考え、\(X \sim 0.7\)とすると
\[\frac{M_\mathrm{max}}{M_\odot} \simeq \sqrt{\frac{4\pi c G}{0.34}} \frac{M}{M_\odot} \simeq 270 \frac{M}{M_\odot} \tag{3}\]のように求まります。 しかし、この値は観測から経験的に得られている値より大きく、実際は\(M \sim 100 - 120 M_\odot\)であることが判明しています。 高温の恒星の有効温度は\(T_\mathrm{eff} \gtrsim 10000 \mathrm{K}\)にも達しますが、このような高温でも重元素の全てがイオン化しているわけではありません。 イオン化していない重元素を考慮すると、先ほどの\(\kappa_\mathrm{el} = 0.2 (1+X)\)より吸収係数が大きくなります。 これにより、ハンフリーズ・デイヴィッドソン限界に一致するような値が得られるとされています。
参考文献
[1] Humphreys & Davidson, 1994, “The Luminous Blue Variables: Astrophysical Geysers”
[2] Esinoza-Galeas et al., 2022, “NICER X-Ray Observations of Eta Carinae during Its Most Recent Periastron Passage”
[3] Weis & Bomans 2020, “Luminous Blue Variables”
[4] NASAウェブサイト, “The Doomed Star Eta Carinae”
[5] Stellar models II: homology
[6] Kippenhahn, Weigert & Weiss, “Stellar Structure and Evolution”
[7] 野本憲一, 定金晃三, 佐藤勝彦, “恒星”