Table of contents
  1. 激しい緩和 (Violent relaxation)
    1. 直感的理解
    2. もう少し詳しい解析
    3. 実際に激しい緩和は起こっているのか？
  2. 参考文献

激しい緩和 (Violent relaxation)

2体緩和で、私たちは銀河のような質量・恒星数の重力多体系は宇宙年齢以上の時間をかけなければ緩和しないことを学びました。 しかし、実際の楕円銀河では緩和が完了していると考えられており、2体緩和以外の別の緩和過程が考えれています。 2体緩和より素早く起こるこの過程を、激しい緩和と呼びます。ここでは激しい緩和について学びましょう。

直感的理解

激しい緩和過程は、重力ポテンシャルが時間に依存して変化する場合に起こりえます。 ここでは重力多体系において、位置\(\mathbf{x}\)にある恒星が感じる重力ポテンシャルを\(\Phi(\mathbf{x}, t)\)のように、時間に陽に依存して書くことにしましょう。 するとこの恒星の全エネルギー\(E = \frac{1}{2} v^2 + \Phi\)の時間変化は

\[\frac{dE}{dt} = \mathbf{v} \cdot \underbrace{\frac{d \mathbf{v}}{dt}}_{= -\frac{\partial \Phi}{\partial \mathbf{x}}} + \frac{\partial \Phi}{\partial \mathbf{x}} \cdot \underbrace{\frac{d\mathbf{x}}{dt}}_{=\mathbf{v}} + \frac{\partial \Phi}{\partial t} = \frac{\partial \Phi}{\partial t} \tag{5}\]

のように書かれます。このことから、恒星の全エネルギーははポテンシャルの時間変化に応じて時間変化することがわかります。 これは下図のように考えることができます。全ての粒子が一定の速度\(v\)を持つ重力多体系を考えましょう。 この多体系の重力ポテンシャルエネルギーが時間変化を起こさなければ、エネルギー保存則から、左から重力ポテンシャルの谷底に入った粒子は同じエネルギーで右側に到達します(上パネル)。 しかし物質やダークマターが集まるなどして、重力ポテンシャルの谷底が深くなった場合には、左から谷底に入ったときに比べて低いエネルギーで右側に到達します(中パネル)。 同様に物質が恒星風や超新星爆発などで吹き飛ばされ、重力ポテンシャルの谷底が浅くなった場合には、左から谷底に入ったときに比べて高いエネルギーで右側に到達します(下パネル)。

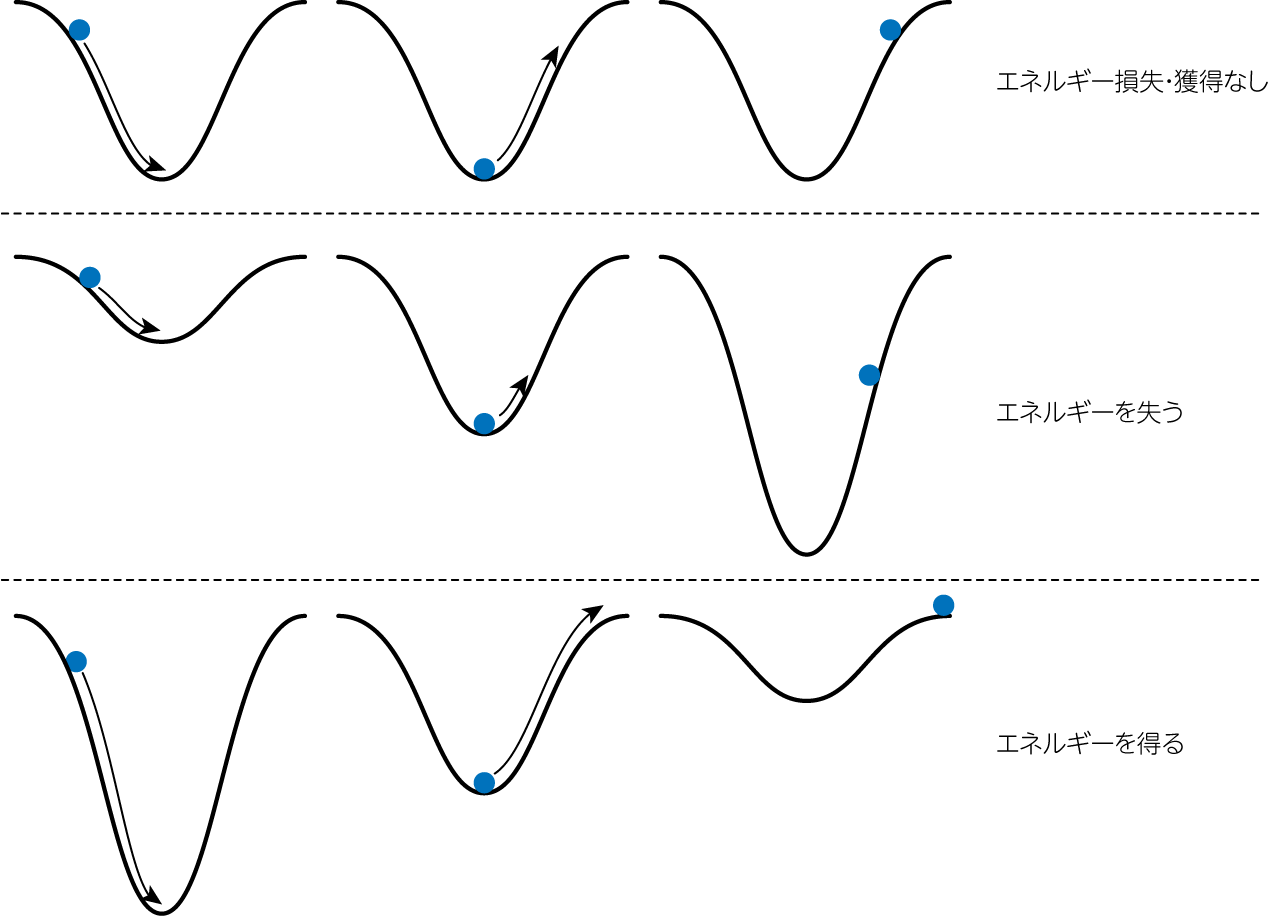
このようにして、一定の速度\(v\)でいたはずの多体系は様々なエネルギーを持つ系に緩和されていくことがわかります。これが激しい緩和の直感的な理解です。

もう少し詳しい解析

それでは激しい緩和過程を導出していきましょう。そのためには、以下のような時間を定義します。

\[t_\mathrm{vr} \equiv \left\{ \frac{\left( \frac{dE}{dt} \right)^2 }{E^2}\right\}^{-1/2} \tag{6}\]

これはエネルギーが時間変化する典型的なタイムスケールを表現したものです。2乗になっているのは、\(\frac{dE}{dt}\)が負になる可能性も考慮しているためです。 全エネルギーは

\[E = \frac{1}{2} m \sum_i \mathbf{v}_i^2 + \frac{1}{2} m \sum_i \sum_{j\neq i}\Phi_{ij} = \mathcal{T} + \mathcal{V} \tag{7}\]

と書けます。ここで\(\Phi_{ij}\)は\(i\)番目の粒子が\(j\)番目の粒子から感じる重力ポテンシャルです。 また簡単のため、この多体系を構成する粒子の質量は全て等しく\(m\)としました。 この両辺を時間で微分すると

\[\begin{align} \frac{dE}{dt} &= m \sum_i \mathbf{v}_i \cdot \underbrace{\frac{d\mathbf{v}_i}{dt}}_{= - \frac{\partial }{\partial \mathbf{x}_i} \sum_{j\neq i} \Phi_{ij}} + \frac{1}{2} m \sum_i \sum_{j\neq i} \frac{\partial}{\partial \mathbf{x}_i} (\Phi_{ij} + \underbrace{\Phi_{ji}}_{=\Phi_{ij}})\cdot \underbrace{\frac{d \mathbf{x}_i}{d t}}_{= \mathbf{v}_i} + \frac{1}{2} m \sum_i \sum_{j\neq i} \frac{\partial \Phi_{ij}}{\partial t} \notag \\ &= \frac{1}{2} m \sum_i \sum_{j\neq i} \frac{\partial \Phi_{ij}}{\partial t} = \dot{\Phi} \tag{8} \end{align}\]

ここで系の全重力ポテンシャルエネルギーを\(\Phi \equiv \frac{1}{2} m \sum_i \sum_{j\neq i} \Phi_{ij}\)のように置きました。 さらに重力多体系で成り立つビリアル定理より

\[2 \mathcal{T} + \mathcal{V} = 0 \ \Longrightarrow \ m \sum_i \mathbf{v}_i^2 = - \frac{1}{2} m \sum_i \sum_{j\neq i} \frac{\partial \Phi_{ij}}{\partial t} \tag{9}\]

です。ここから、全エネルギーは

\[E = \frac{1}{4} m \sum_i \sum_{j \neq i} \Phi_{ij} = \frac{1}{2} \Phi \tag{10}\]

のように計算されます。(6), (8), (10)式より

\[t_\mathrm{vr} = \frac{1}{2} \left\{ \frac{\dot{\Phi}^2}{\Phi^2}\right\}^{-1/2} \tag{11}\]

のように書けます。

Lynden-Bellの原論文では前の係数が3/4になっている...どこか計算ミスがある？まぁオーダーが一緒なのでとりあえずﾖｼ(๑˃̵ᴗ˂̵)و

(5)式や(11)式の出現した\(\dot{\Phi}\)は、系の全重力ポテンシャルエネルギーの時間変化を表します。 この時間変化のタイムスケールは\(t_\mathrm{cross}\)程度と考えることができるため、結局\(t_\mathrm{vr}\)も\(t_\mathrm{cross}\)と同じオーダーとなります。 ここで2体緩和で緩和までにかかる時間\(t_\mathrm{relax}\)との比較をしてみましょう。すると

\[t_\mathrm{vr} \simeq t_\mathrm{cross} \ll \frac{N}{6 \ln N} t_\mathrm{cross} \tag{12}\]

となり、系の粒子数\(N\)が大きい場合には、\(t_\mathrm{relax}\)より大分短いことがわかります。このことから、この現象を激しい緩和と呼びます。

実際に激しい緩和は起こっているのか？

ここまでくると「宇宙にある銀河や球状星団は2体緩和ではなく激しい緩和により、ある平衡状態に落ち着いている！」と考えてしまうかもしれません。 実際、楕円銀河の表面輝度分布はドゥ・ボークルール則 (de Vaucouleurs’s law)に従うことが知られています。 2体緩和では銀河のような系は緩和するまでに宇宙年齢以上の時間がかかります。 楕円銀河でこのような普遍的な構造を得るためには、2体緩和とは別のメカニズムで緩和していなければならないと考えるのが普通です。
しかし、この激しい緩和過程には疑問が残ります。例えば、重力収縮により銀河が形成されていく過程を考えましょう。 初期には重力によってダークマターや物質が集まり、重力ポテンシャルの底が時間とともに深くなっていくことから、激しい緩和が進むことが考えられます。 しかし一度力学平衡に落ち着いてしまうと、そこからエネルギーの変化は起こらなくなり、激しい緩和は止まるはずです。
リンデンベル (Lynden-Bell)が1967年に激しい緩和を提唱してから今日に至るまでに、計算機の発展とともに様々な数値実験が行われてきました。 現在では、初期条件によって終状態は様々であり、ある一つの緩和した状態に向かうとは到底言えないというのが共通認識として知られています。
では2体緩和が正しいということになるのでしょうか。 2体緩和は、重力相互作用により速度の変化が起こることで緩和へと向かう過程です。 するとエネルギー等分配により、運動エネルギーが全ての粒子で同じ程度になるくらいまで系が進化していきます。 すると\(\frac{1}{2} m v^2 \sim (定数)\)のようになるため、質量の大きい粒子ほど速度は遅くなり、重力多体系の中心部に落ちていきます。 結果として、外側には比較的質量の軽い粒子が、そして内側には質量の重たい粒子が集まることになります(下図参照)。 このような現象を質量分離 (mass segregation)と呼びます。

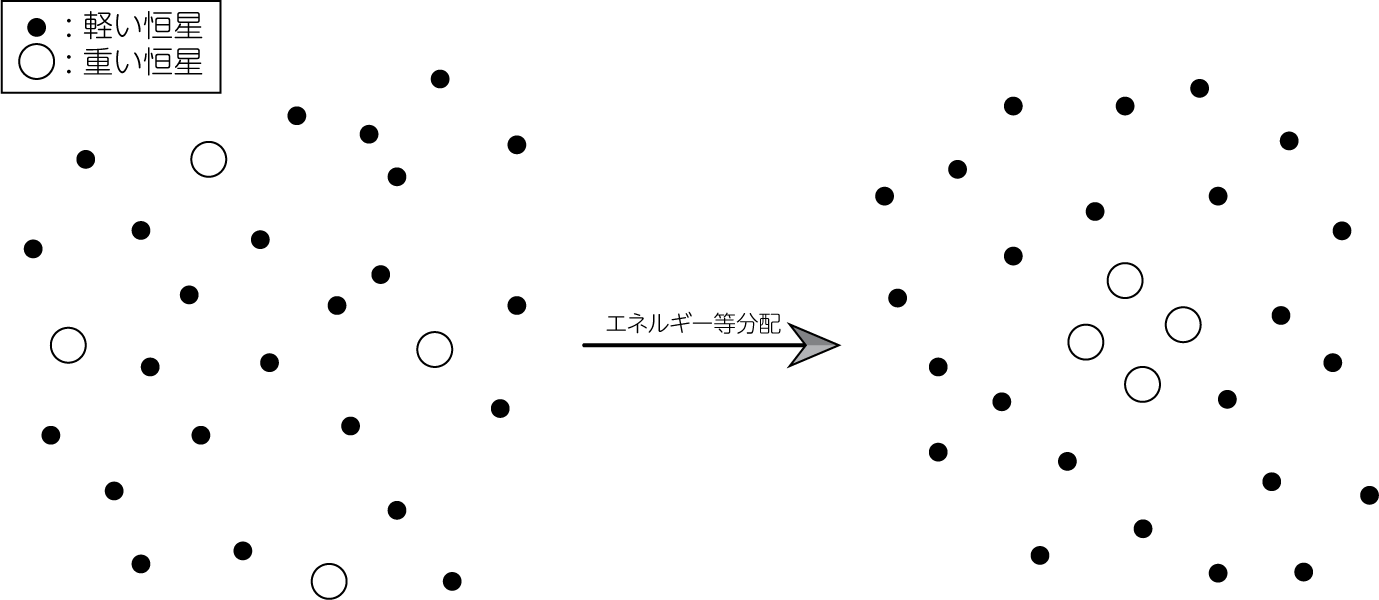
一方、激しい緩和過程では

\[m \frac{d\mathbf{v}}{dt} = - m \frac{\partial \Phi}{\partial \mathbf{x}} \ \Longrightarrow \ \frac{d\mathbf{v}}{dt} = - \frac{\partial \Phi}{\partial \mathbf{x}}\]

から、(重力の等価性より)質量に依存せず、等しくポテンシャルの時間変化を感じることができます。よって2体緩和のような質量分離は起こりません。
星団を観測し、質量分離が起こっているかどうかを判定することで、2体緩和が優先的に起こっているのか、それとも激しい緩和が起こっているのかを知ることができます。 実際の(球状・散開を含む)星団のシミュレーションと観測では、質量分離の度合いは様々なようです。 「質量分離を起こしている証拠はない」とする論文もあれば、「質量分離の具合から星団の進化がわかる」とする論文も見られ、現在でもそう単純にどちらが支配的かを決定するのは難しいとされています。 また星団の中にさらに小さな集団(subcluster)が存在するような系も発見されており、星団の緩和過程は今なお最先端の研究分野となっています。 また質量分離から重たい恒星が中心部に集まれば、そこで重たい恒星どうしが連星系を成し、最終的にブラックホール連星になることが予想されます。 このように、星団からの重力波の検出を目指す研究も盛んに行われています。

参考文献

Copyright © github-nakasho