Table of contents
スペクトル線
ここでは、恒星からの光の観測にたびたび現れるスペクトル線(輝線・吸収線)についてメモします。
スペクトル線の観測量
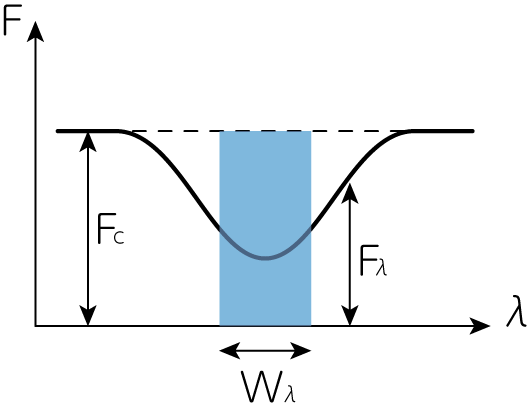
恒星のスペクトルは光の波長または振動数に対するflux(太陽ではintensity)分布を表します。 吸収線の深さは吸収線内の波長\(\lambda\)でのflux \(F_\lambda\)と、連続スペクトルのflux \(F_c\)を用いて
\[A_\lambda = \frac{F_c - F_\lambda}{F_c} = 1 - \frac{F_\lambda}{F_c} \tag{5.1}\]のように定義されます。 そしてresidual fluxとして
\[R_\lambda = \frac{F_\lambda}{F_c} = 1-A_\lambda \tag{5.2}\]を定義します。
スペクトル線の強さを表すために等価幅(equivalent width)
がよく用いられます。 等価幅は、吸収線の底でのfluxがゼロの短冊型としたときの幅に等しく、その吸収線により吸収された全エネルギーを示す量となります。 もちろん、等価幅は振動数単位でも表すことができます。
\[W_\nu = \int_0^\infty A_\nu d\nu, \quad \frac{W_\nu}{\nu_0} = \frac{W_\lambda}{\lambda_0} \tag{5.4}\]ここで\(\lambda_0, \nu_0\)はそれぞれ吸収線の中心での波長と周波数です。
Eddington-Barbier関係とLTEの近似 \(S_\nu (\tau_\nu) = B_\nu (\tau_\nu)\) を用いると、恒星から出てくるfluxは
\[F_\nu (0) \simeq \pi B_\nu (2/3)\]のようになるのでした。これは\(\tau_\nu \simeq 2/3\)の場所の源泉関数(今の場合はプランク関数)に比例する、ということを意味します。 光学的厚み\(\tau_\nu\)は大雑把に\(D(\rho) \kappa_\nu \simeq m \kappa_\nu\)のように表されます(\(dm = -\rho dz = \frac{d\tau_\nu}{\kappa_\nu + \sigma_\nu}\), \(m\)は大気の外側からその層までに含まれる質量です。) ここから、振動数\(\nu\)のflux \(F_\nu(0)\)は\(m \simeq 2/(3\kappa_\nu)\)の場所の黒体放射\(B_\nu\)に等しくなります。 吸収線内の振動数では\(\kappa_\nu\)が大きく、外側の温度の低い場所の光を見ていることになるため、暗くなり、吸収線として観測されるのです。