Table of contents
吸収線吸収係数
一般に、吸収線は広がりを持ちます。 これは関与するエネルギー準位の寿命が有限であるために、その準位が有限の幅を持つことが原因です。 さらに原子・イオンの熱運動や、恒星の自転などの大規模な運動によるドップラー効果などが原因のものがあります。 エネルギー準位の幅に起因する吸収線の広がりには、エネルギー準位からの遷移自体に起因するnatural (or radiation) dampingと、他粒子との衝突によって起こるpressure broadeningとがあります。
Natural damping profile
古典振動子による議論
以前、古典振動子が強制振動することにより光を放出する場合、ローレンツ型の輝線プロファイルができることを示しました。 ここでは、減衰振動する振動子からも同様のローレンツプロファイルができることを示しましょう。 外場がないときの減衰振動の運動方程式は
\[\ddot{x} = -\omega_0^2 x - \gamma \dot{x} \tag{5.5}\]と書かれます。 ここで、\(\gamma\)は古典振動子を表す定数で
\[\gamma \equiv \frac{2e^2 \omega_0^2}{3 m c^3} \tag{5.6}\]で与えられます。 減衰項である\(\gamma \dot{x}\)は、振動項\(\omega_0^2 x\)に比べて非常に小さいため、\(\gamma \dot{x} \simeq i \omega_0 \gamma x\)のように近似することができます。 よって(5.5)式は
\[\ddot{x} = - (\omega_0^2 + i\gamma \omega_0) x \tag{5.7}\]のように書き直せます。 \(\gamma^2\)は無視すると、(5.7)式の解は
\[x = x_0 e^{-\gamma t /2} e^{i\omega_0 t} \tag{5.8}\]となります。 これは指数関数的に振幅が減少する振動です。 \(t = 0\)から急激に振動が始まった仮定して、この振動のフーリエ変換を計算しましょう。 すると
\[F(\omega) = \frac{x_0}{\sqrt{2\pi}} \int_0^\infty e^{-i(\omega - \omega_0) t} e^{-\gamma t / 2} dt = \frac{1}{\sqrt{2\pi}}\frac{x_0}{i(\omega - \omega_0) + \gamma / 2} \tag{5.9}\]を得ます。 したがって、エネルギースペクトル\(E(\omega) = F^\ast(\omega) F(\omega)\)は
\[E(\omega) = \frac{x_0^2 / 2\pi}{(\omega - \omega_0)^2 + (\gamma / 2)^2} \tag{5.10}\]となります。 この関数を規格化した形は
\[I(\omega) = \frac{\gamma / 2\pi}{(\omega - \omega_0)^2 + (\gamma / 2)^2} \qquad \left( \int_{-\infty}^\infty I(\omega) d\omega = 1\right)\tag{5.11}\]です。 このように、減衰振動する振動子はローレンツプロファイルを作り、そのfull half-intensity width (強度が半分になる幅)が\(\gamma\)となります。
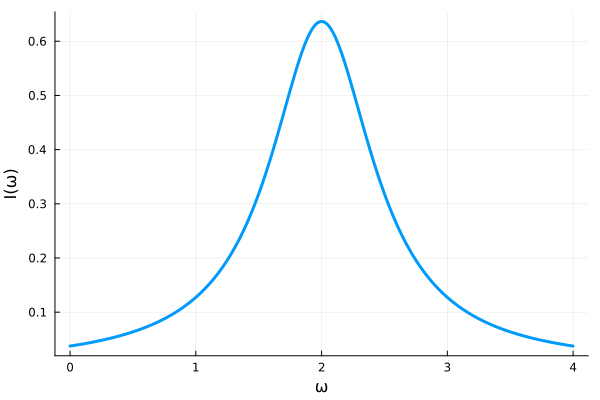
これを波長で表すと、\(\lambda = 2\pi c / \omega \Longrightarrow \delta \lambda = -2\pi c \Delta \omega / \omega^2\)より
\[\Delta \lambda_c = \frac{2\pi c \gamma}{\omega^2} = \frac{4\pi e^2}{3 m c^2} \sim 1.2 \times 10^{-4} \ [\mathring{\mathrm{A}}] \tag{5.12}\]となります。 この幅は、実験室や実際に天体で観測されるスペクトル線幅よりも格段に小さな値です。 したがって、実際のスペクトル線幅を理解するためには、他の物理過程を考える必要がります。
量子力学からの考察
原子またはイオンからの放射を量子力学的に解釈すると、これはある励起状態から下のエネルギー準位への遷移に伴うものと考えることができます。 この放射過程は、WeisskoptとWignerにより、1930年に量子力学的に記述されたようです。 励起状態\(j\)から、それよりエネルギーの低い状態\(i\)への遷移確率が
\[\frac{dN_j}{dt} = - \Gamma N_j\]で与えられるとしましょう。 イオンが状態\(j\)になっている確率\(P_j (t)\)は、\(j\)状態の波動関数\(\psi_j (r, t)\)を用いて
\[P_j (t) = \psi_j^\ast \psi_j e^{-\Gamma t} \tag{5.13}\]のように書くことができます。 ここで、\(\Gamma\)はspontaneous emission(自然放射)のアインシュタイン係数\(A_{ji}\)に等しいものです(\(\Gamma = A_{ji}\)。) この式は、状態\(j\)の波動関数の時間発展が
\[\psi_j (\mathbf{r}, t) e^{-\Gamma t / 2} = u_j (\mathbf{r}) e^{-i E_{ji} t / \hbar} e^{-\Gamma t / 2} = u_j (\mathbf{r}) e^{-(i \omega_{ji} + \Gamma /2) t} \tag{5.14}\]のように書けることを示しています。 ここで\(E_{ji} = E_j - E_i = \hbar \omega_{ji}\)です。 (5.14)式は、状態\(j\)のエネルギーが\(\Delta E_j \simeq \hbar \Gamma\)程度の幅の広がりを持つことを表しています。 状態\(j\)の寿命は、遷移確率の逆数\(\Delta t_j \simeq 1 / \Gamma\)程度なので
\[\Delta E_j \simeq \hbar \Gamma \simeq \frac{\hbar}{\Delta t_j} \tag{5.15}\]のように書くことができます。 これは量子力学の不確定性原理に一致します。 そしてこの式は、放射される光の振動数に幅があることを意味します。 振幅のスペクトル(\(\omega\)に対する振幅の分布)は(5.14)式のフーリエ変換を計算すれば求めることができます。 さらにエネルギースペクトルはその絶対値の2乗です。
(5.14)式は、古典的な振動子の式(5.8)と同じ形をしています。 よって得られるエネルギースペクトルは、同じくローレンツ型の
となります。 高いエネルギーにある状態からの遷移は、一般には\(i\)状態以外への遷移も存在します。 また低いエネルギー準位である\(i\)も種々の遷移によって幅を保つため、\(\Gamma\)はそれらの総和
\[\Gamma = \Gamma_U + \Gamma_L, \qquad \Gamma_U = \sum_k A_{jk}, \qquad \Gamma_L = \sum_k A_{ik} \tag{5.17}\]と考えた方が良いでしょう。

このようにして求められた線輪郭は輝線に対するものですが、定常状態においては吸収と発光が釣り合っていなければならないという条件\(\kappa_\nu B_\nu = \eta_\nu^t\)から、吸収線も同じ形を持つことがわかります。 ここから、吸収線に対する原子一個あたりの吸収係数\(\alpha_\nu\)を計算することにしましょう。 この量に変換するには、振動子強度(oscillator strength)を用いて
\[\alpha_\nu = \frac{\pi e^2}{m c} f \frac{\Gamma / (2\pi)^2}{(\nu - \nu_0)^2 + (\Gamma / 4\pi)^2} \tag{5.18}\]のように表されます。 吸収線全体の吸収は
\[\int_0^\infty \alpha_\nu d\nu = \frac{\pi e^2}{m c} f \tag{5.19}\]です。 このような放射減衰による吸収線は密度が非常に薄い場所で形成されるような、強い吸収線で重要となります。 しかし通常の恒星大気では、次に述べるような圧力による吸収線の広がり(pressure broadning)が重要な影響を持ちます。
熱運動による影響(Thermal Doppler Broadening): フォークト関数
個々の粒子は熱運動をしているため、実際に観測される吸収線はドップラー効果によって少しずつ波長のずれた吸収線の重ね合わせとして観測されます。 マクスウェル分布をする粒子形において、視線速度\(\xi\)が\((\xi , \xi + d\xi)\)の範囲にある確率は
\[W(\xi) d\xi = \frac{1}{\sqrt{\pi} \xi_0} e^{-\xi^2 / \xi_0^2} d\xi \tag{5.20}\]で表されます。 ここで
\[\xi_0 = \sqrt{ \frac{2k_B T}{m_i}} = 12.85 \sqrt{\frac{T/(10^4 \ \mathrm{K})}{A}} \quad [\mathrm{km / s}] \tag{5.21}\]です。 \(A\)は原子質量数を表し、途中の変形では\(10^4\)Kが1eVであることを用いました。
観測される光の振動数を\(\nu\)とすると、視線速度\(\xi\)を持つ原子はドップラー効果により\(\nu (1-\xi / c)\)の振動数の光として吸収します。 よって、対応する吸収係数は\(\alpha (\nu - \xi \nu / c )\)になります。 (5.20)式の分布に従って、様々な視線速度を持つ原子が存在するため、この系全体による吸収係数は
の様に表されます。 (5.22)式に(5.20), (5.18)式を代入しましょう。
\[\alpha_\nu = \frac{\pi e^2 f}{mc} \frac{\Gamma}{(2\pi)^2} \frac{1}{\xi_0 \sqrt{\pi}} \int_{-\infty}^\infty d\xi \frac{e^{-\xi^2 / \xi_0^2}}{\left( \nu - \frac{\xi}{c} \nu - \nu_0 \right)^2 + \left( \frac{\Gamma}{4\pi} \right)^2}\]この式の分母を整理しましょう。 このとき、視線速度が\(\xi \ll c\)であることから、\(\frac{\xi}{c} \nu \simeq \frac{\xi}{c} \nu_0\)のように近似できるとすると
\[\left( \nu - \frac{\xi}{c} \nu - \nu_0 \right)^2 \simeq \left( \nu - \frac{\xi_0 \nu_0 }{c} \frac{\xi}{\xi_0} - \nu_0 \right)^2 = \left( \nu - \nu_0 - \Delta \nu_D \frac{\xi}{\xi_0} \right)^2 = (\Delta \nu_D)^2 \left( v - y \right)^2\]のように変形されます。途中
\[\Delta \nu_D \equiv \frac{\xi_0 \nu_0}{c}, \quad v \equiv \frac{\nu - \nu_0}{\Delta \nu_D}, \quad y \equiv \frac{\xi}{\xi_0} \tag{5.23}\]を用いました。 さらに\(a \equiv \frac{\Gamma}{4\pi \Delta \nu_D}\)を定義すれば
\[\begin{align} \alpha_\nu &= \frac{\pi e^2 f}{mc} \frac{\Gamma}{4\xi_0 \pi^2 \sqrt{\pi}} \int_{-\infty}^\infty dy \frac{e^{-y^2} \xi_0}{(\Delta \nu_D)^2 \left( v-y \right)^2 + (\Delta \nu_D)^2 a^2} \notag \\ &= \frac{\sqrt{\pi} e^2 f}{mc \Delta \nu_D} \frac{a}{\pi} \int_{-\infty}^\infty dy \frac{e^{-y^2}}{\left( v-y \right)^2 + a^2} = \frac{\sqrt{\pi} e^2 f}{mc \Delta \nu_D} H(a, v) \tag{5.24} \end{align}\]のように整理されます。 ここで
\[H(a, v) = \frac{a}{\pi} \int_{-\infty}^\infty \frac{e^{-y^2}}{(v-y)^2 + a^2} dy \tag{5.25}\]は、フォークト関数(Voigt function)として知られるものです。 また、途中で出てきた\(a\)は減衰係数と呼ばれるもので、恒星大気では\(a \ll 1\)であることが知られています。 このことから\(H(a, v)\)を\(a\)でテイラー展開することを考えましょう。 まず、\(\cos\)関数のラプラス変換を計算すると
\[\int_0^\infty e^{-ax} \cos (bx) dx = \frac{a}{a^2 + b^2} \tag{5.26}\]のようになります。 これを用いるとフォークト関数は
\[\begin{align} H(a, v) &= \frac{1}{\pi} \int_{-\infty}^\infty dy e^{-y^2} \int_0^\infty dx e^{-ax} \cos \{(v-y) x \} \notag \\ &= \frac{1}{\pi} \int_{0}^\infty dx e^{-ax} \int_{-\infty}^\infty dy e^{-y^2} \{ \cos (vx) \cos (xy) + \sin(vx) \sin(xy) \} \notag \\ &= \frac{1}{\pi} \int_0^\infty dx e^{-ax} \cos (vx) \int_{-\infty}^\infty dy e^{-y^2} \cos (xy) \tag{5.27} \end{align}\]のように変形されます。 途中、\(e^{-y^2} \sin (xy)\)は\(y\)の奇関数であることから、\(\int_{-\infty}^\infty\)での積分値がゼロとなることを用いました。 次にガウス関数のcos変換が
\[\int_{-\infty}^\infty e^{-y^2} \cos (xy) dy = \sqrt{\pi} e^{-x^2 / 4} \tag{5.28}\]と書けることを用いると、(5.27)式は
\[H(a, v) = \frac{1}{\sqrt{\pi}} \int_0^\infty e^{-\{ax + (x^2 / 4)\}} \cos (vx) dx \tag{5.29}\]のようになります。 ここで\(a \ll 1\)として、\(e^{-ax} = \sum_{n=0}^\infty (-1)^n a^n x^n / (n!)\)を用いましょう。 すると
\[H(a, v) = a^n H_n (v) \qquad \left( H_n (v) \equiv \frac{(-1)^n}{\sqrt{\pi} n!} \int_0^\infty x^n e^{-x^2/4} \cos (vx) dx \right) \tag{5.30}\]のように表現されます。 具体的に\(H_0(v), H_1(v)\)を計算しましょう。
\[H_0(v) = \frac{1}{\sqrt{\pi}} \int_0^\infty e^{-x^2/4} \cos (vx) dx \underbrace{=}_{(5.28)} e^{-v^2} \tag{5.31}\] \[\begin{align} H_1 (v) &= - \frac{1}{\sqrt{\pi}} \int_0^\infty x e^{-x^2 /4} \cos (vx) dx = - \frac{1}{\sqrt{\pi}} \left\{ -2 [e^{-x^2 / 4} \cos (vx)]_0^\infty - 2v \int_0^\infty e^{-x^2 / 4} \sin (vx) dx \right\} \notag \\ &= - \frac{2}{\sqrt{\pi}} \left\{ 1 - v \int_0^\infty e^{-x^2 /4} \sin (vx) dx \right\} \tag{5.32} \end{align}\]さらにガウス関数のsin変換
\[\int_0^\infty e^{-y^2} \sin (2vy) dy = e^{-v^2} \int_0^v e^{y^2} dy \equiv F(v) \tag{5.33}\]を用いれば、(5.32)式は
\[H_1 (v) = \frac{2}{\sqrt{\pi}} \{2v F(v) -1\} \tag{5.34}\]のようになります。 ここで、関数\(F(v)\)はダーソンの積分関数(Dawson’s integral)として知られています。 \(v \gg 1\)のとき、\(H(a, v) \simeq a / (\sqrt{\pi} v^2)\)と近似できるため(後述の補遺参照)、このときのフォークト関数は
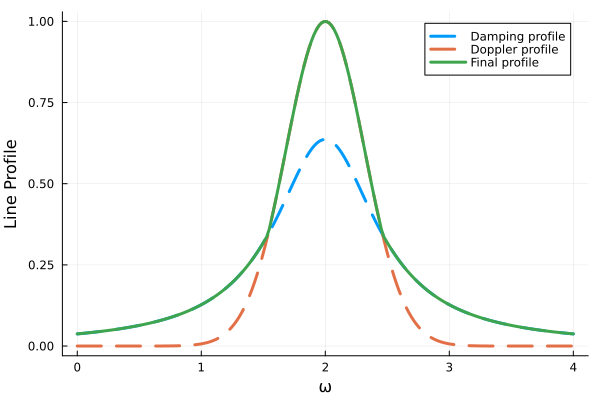
\[H(a, v) \simeq \left\{ \begin{array}{ll} e^{-v^2} & (v \ll 1)\\ \frac{a}{\sqrt{\pi} v^2} & (v \gg 1) \end{array} \right.\]よって吸収線の中心部\(v = \nu - \nu_0 / \Delta \nu_D \simeq 0\)ではドップラー効果による\(e^{-y^2}\) (Doppler core)が優勢で、吸収線の端 (line wing)では\(a / (\sqrt{\pi} v^2)\) (damping profile)が優勢となります。 吸収線中心部のドップラーコアと呼ばれる部分は、その形がボルツマン分布にも似ていることから、熱的な影響と考えることができます。 これまでの議論から、吸収線の概形は下図緑線のようになります。
補遺1: cos関数のラプラス変換
\[\begin{align} \int_0^\infty e^{-ax} \cos (bx) dx &= \frac{1}{2} \int_0^\infty dx \{ e^{-(a-ib) x} +e^{-(a+ib) x}\} = \frac{1}{2} \left[ - \frac{e^{-(a-ib) x}}{a-ib} - \frac{e^{-(a+ib) x}}{a+ib} \right]_0^\infty \notag \\ &= \frac{1}{2} \left( \frac{1}{a-ib} + \frac{1}{a+ib} \right) = \frac{a}{a^2 + b^2} \tag{*.1} \end{align}\]補遺2: ガウス関数のcos変換
\[\int_{-\infty}^\infty dy e^{-y^2} \cos (yx) = \int_{-\infty}^\infty dy \frac{e^{-y^2 + iyx} + e^{-y^2 - iyx}}{2} = \int_{-\infty}^\infty dy e^{-y^2 - iyx}\]ここで、最後の等号の式変形では、\(y\)の符号を反転させても同じ形になることを用いました。 さらに計算を進めると
\[\int_{-\infty}^\infty dy e^{-y^2 - iyx} = \underbrace{\int_{-\infty}^\infty dy e^{-(y - ix/2)^2}}_{複素積分} e^{-x^2 / 4} = \sqrt{\pi} e^{-x^2 / 4} \tag{*.2}\]途中の複素積分の部分は、ガウス積分の親戚のようにも見えることから\(\sqrt{\pi}\)になりそうな気がします。 しかしここでは、より厳密に複素数平面上での積分からこれを示してみましょう。 被積分関数を\(e^{-z^2} \ (z = \eta + i\zeta)\)のように書き、これを下図のような複素数平面上の経路で積分することを考えましょう。
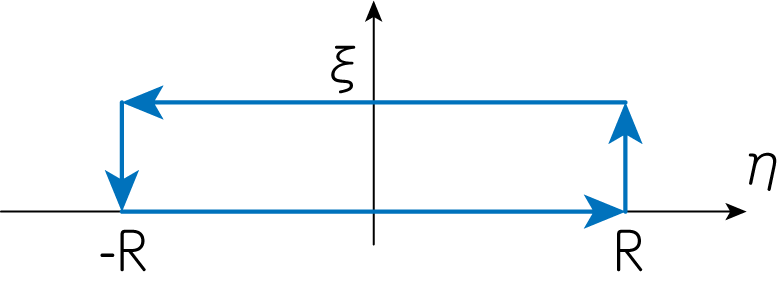
この積分経路の内側の至る所で、この関数は正則です。 よって留数定理より
\[\oint_C dx e^{-z^2} = 0\]この左辺は
\[\int_{-R}^R d\eta e^{-\eta^2} + \int_0^\zeta d\zeta i e^{-(R+i\zeta)^2} + \int_R^{-R} d\eta e^{-(\eta + i\zeta)^2} + \int_\zeta^0 i e^{-(-R+i\zeta)^2}\]のように変形することができます。 これを\(R \rightarrow \infty\)の極限をとると、2項目と4項目はゼロになります。 よって
\[\int_{-\infty}^\infty d\eta e^{-\eta^2} - \int_{-\infty}^\infty d\eta e^{-(\eta + i\zeta)^2} = 0 \ \Longrightarrow \ \int_{-\infty}^\infty d\eta e^{-(\eta + i\zeta)^2} = \int_{-\infty}^\infty d\eta e^{-\eta^2} \underbrace{=}_{ガウス積分} \sqrt{\pi} \tag{*.3}\]を得ます。
補遺3: フォークト関数の性質
(5.25)式を、\(v : -\infty \rightarrow \infty\)の範囲で積分してみましょう。
\[\int_{-\infty}^\infty H(a, v) dv = \frac{a}{\pi} \int_{-\infty}^\infty \left( \int_{-\infty}^\infty \frac{e^{-y^2}}{(v-y)^2 + a^2} dy\right) dv = \frac{a}{\pi} \int_{-\infty}^\infty e^{-y^2} \left( \int_{-\infty}^\infty \frac{dv}{(v-y)^2 + a^2}\right) dy\]ここで\(v-y = x\)とすると
\[\int_{-\infty}^\infty H(a, v) dv = \frac{a}{\pi} \int_{-\infty}^\infty e^{-y^2} \left( \int_{-\infty}^\infty \frac{dx}{x^2 + a^2}\right) dy\]のようになります。 さらに\(x = a \tan \theta\)のように変換を行えば
\[\int_{-\infty}^\infty H(a, v) dv = \frac{a}{\pi} \int_{-\infty}^\infty e^{-y^2} \left( \frac{1}{a^2} \int_{-\pi/2}^{\pi/2} \frac{\frac{a}{\cos^2 \theta} d\theta}{\tan^2 \theta + 1}\right) dy = \int_{-\infty}^\infty e^{-y^2} dy \underbrace{=}_{ガウス積分} \sqrt{\pi} \tag{*.4}\]と計算されます。 次に、(5.30)式で定義された\(H_n (v)\)の満たす漸化式を証明してみましょう。 \(n \rightarrow n-2\)の\(v\)での微分を計算すると
\[H_{n-2} (v) = \frac{(-1)^{n-2}}{\sqrt{\pi} (n-2)!} \int_0^\infty x^{n-2} e^{-x^2/4} \cos (vx) dx\]より
\[\frac{dH_{n-2}}{dv} = \frac{(-1)^{n-2}}{\sqrt{\pi} (n-2)!} \int_0^\infty x^{n-2} e^{-x^2/4} (-x) \sin (vx) dx\]を得ます。 さらにもう一度、\(v\)で微分すると
\[\begin{align} \frac{d^2H_{n-2}}{dv^2} &= \frac{(-1)^{n-2}}{\sqrt{\pi} (n-2)!} \int_0^\infty x^{n-2} e^{-x^2/4} (-x^2) \cos (vx) dx = - \frac{n(n-1)}{(-1)^2} \frac{(-1)^n}{\sqrt{\pi} n!} \int_0^\infty x^n e^{-x^2/4} \cos (vx) dx \notag \\ &= -n(n-1) H_n(v) \notag \end{align}\]となることから
\[H_n(v) = - \frac{1}{n(n-1)} \frac{d^2 H_{n-2}}{dv^2} \tag{*.5}\]とわかります。 この漸化式を用いて、より高次の\(H_n(v)\)を具体的に計算してみましょう。
\[H_2 (v) = -\frac{1}{2 \cdot 1} \frac{d^2 H_0}{dv^2} \underbrace{=}_{(5.31)} -\frac{1}{2} \frac{d}{dv} (-2v e^{-v^2}) = e^{-v^2} + v (-2v) e^{-v^2} = e^{-v^2} (1-2v^2) \tag{*.6}\]次は\(H_3\)の計算です。 このために\(F\)の微分を計算すると
\[\frac{dF}{dv} \underbrace{=}_{(5.33)} (-2v) e^{-v^2} \int_0^v e^{y^2} dy + e^{-v^2} e^{v^2} = -2v F(v) + 1\] \[\frac{d^2F}{dv^2} = -2 \left\{ F(v) + v \frac{dF}{dv} \right\} = -2 \left\{ F(v) + v (-2v F(v) + 1) \right\} = -2 \left\{ (1-2v^2) F(v) + v\right\}\]となります。 これらより
\[\begin{align} H_3(v) &= - \frac{1}{3 \cdot 2} \frac{d^2 H_1}{dv^2} \underbrace{=}_{(5.34)} - \frac{1}{3\sqrt{\pi}} \frac{d^2}{dv^2} (2vF(v) -1) = -\frac{1}{3\sqrt{\pi}} \frac{d}{dv} \left( 2 F(v) + 2v \frac{dF}{dv} \right) \notag \\ &= -\frac{2}{3\sqrt{\pi}} \left( \frac{dF}{dv} + \frac{dF}{dv} + v \frac{d^2 F}{dv^2} \right) = -\frac{2}{3\sqrt{\pi}} [ 2(-2v F(v) +1) + v (-2) \{(1-2v^2) F(v) + v\} ] \notag \\ &= - \frac{4}{3 \sqrt{\pi}} \{ (2v^2-3) v F(v) - v^2 + 1\} \tag{*.7} \end{align}\]と求まります。 最後に\(H_4\)を計算しましょう。
\[\begin{align} H_4 (v) &= - \frac{1}{4 \cdot 3} \frac{d^2 H_2}{dv^2} = - \frac{1}{12} \frac{d}{dv} \{ -2v e^{-v^2} (1-2v^2) + e^{-v^2} (-4v) \} = \frac{1}{6} \frac{d}{dv} \{ (-2v^3 + 3v) e^{-v^2}\} \notag \\ &= \frac{1}{6} \{ (-6v^2 + 3) e^{-v^2} + (-2v^3 + 3v) (-2v) e^{-v^2}\} = \frac{1}{6} (4v^4 - 12 v^2 + 3) e^{-v^2} \tag{*.8} \end{align}\]最後に、フォークト関数の近似形を導出しましょう。
\[H(a, v) = \frac{a}{\pi} \int_{-\infty}^\infty \frac{e^{-y^2}}{v^2 + a^2 - 2vy + y^2} dy = \frac{a}{\pi} \frac{1}{v^2 + a^2} \int_{-\infty}^\infty \frac{e^{-y^2}}{1 + \frac{v^2 - 2vy}{v^2 + a^2}} dy\]\(v^2 + a^2 \gg 1\)のとき
\[H(a, v) \simeq \frac{a}{\pi} \frac{1}{v^2 + a^2} \int_{-\infty}^\infty e^{-y^2} dy \underbrace{=}_{ガウス積分} \frac{a}{\sqrt{\pi}} \frac{1}{v^2 + a^2} \tag{*.9}\]よって、さらに\(v \gg 1\)ならば、\(H(a, v) \simeq a / (\sqrt{\pi} v^2)\)と近似されることがわかります。
補遺4: フォークト関数の可視化
最後に、\(a = 1.0, 0.1, 0.01, 0.001\)に対する\(\log_{10} H(a, v)\)を\(v\)の関数として図示します。
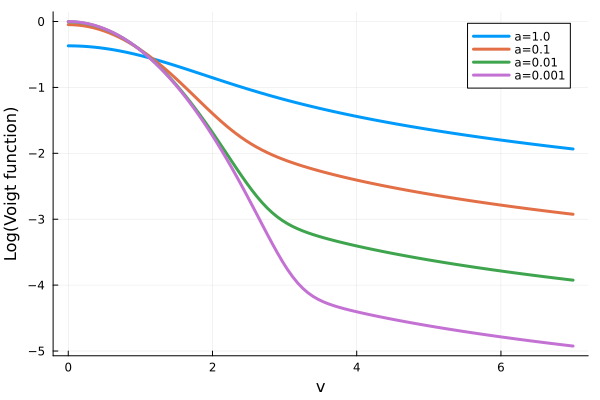
また、図示に用いたJuliaスクリプトを以下に示します。
using QuadGK
using Plots
gr()
# define the integrand funciton for Voigt function
function f(a, v, x)
return exp(-(a*x+x^2/4)) * cos(v*x)
end
# set array for a
array_a = [1, 0.1, 0.01, 0.001]
# get length of array_a
len_a = length(array_a)
# set length of v
len_v = 100
# set array for v
array_v = range(0.0, 7.0, length=len_v)
# initialize an array for Voigt function
voigt = zeros(Float64, len_a, len_v)
for i in 1:len_a
a = array_a[i]
for j in 1:len_v
v = array_v[j]
# compute integration using quadgk
integral, error = quadgk(x -> f(a, v, x), 0, 100)
# put the integration result into voigt array
voigt[i, j] = log10(integral/sqrt(pi))
end
end
# visualize Voigt function for each a
plot(array_v, voigt[1, :], linewidth=3, xlabel="v", ylabel="Log(Voigt function)", label="a=1.0")
plot!(array_v, voigt[2, :], linewidth=3, label="a=0.1")
plot!(array_v, voigt[3, :], linewidth=3, label="a=0.01")
plot!(array_v, voigt[4, :], linewidth=3, label="a=0.001")
savefig("absorption_line_coeff_04.png")