ヘリウム燃焼

例として、ここではヘリウム燃焼により\({}^4 \mathrm{He}\)から\({}^{12} \mathrm{C}, {}^{16} \mathrm{O}\)を生成することを考えましょう。ここではトリプルアルファ反応により\({}^{12} \mathrm{C}\)を生成し、そこにさらに\({}^4 \mathrm{He}\)を追加することで\({}^{16} \mathrm{O}\)を生成します。さらに\({}^{20} \mathrm{Ne}\)を作るために、\({}^{16} \mathrm{O}\)が破壊される反応も考慮に入れましょう。この核融合反応が起こる場所は中質量星の中心部であるとし、\(\rho = 10^4 \mathrm{g/cm^3}, T_9 = 0.15\)とします。ヘリウム、炭素、酸素、ネオンの数密度をそれぞれ\(N_4, N_{12}, N_{16}, N_{20}\)とし、さらにそれぞれの質量比を\(X_4, X_{12}, X_{16}, X_{20}\)とします。またここで考慮する核融合反応での、散乱断面積と速度の積の平均\(\langle \sigma v \rangle\)を、以下のように書きます。

トリプルアルファ反応: \(\langle 3\alpha \rangle\)
\({}^{12} \mathrm{C} (\alpha, \gamma) {}^{16} \mathrm{O}\): \(\langle \alpha12 \rangle\)
\({}^{16} \mathrm{O} (\alpha, \gamma) {}^{20} \mathrm{Ne}\): \(\langle \alpha16 \rangle\)

各元素の数密度が満たす微分方程式

これらを用い、\(N_4, N_{12}, N_{16}, N_{20}\)が満たす微分方程式を書き下していきましょう。まずは\(N_4\)についてです。トリプルアルファ反応では、まず\({}^4 \mathrm{He} + {}^4 \mathrm{He}\)による反応が起こり、\({}^8 \mathrm{Be}\)が生成されます。するとこの反応の反応断面積を\(\sigma_{2\alpha}\)とすると、単位体積・単位時間あたりの反応数は\(\frac{1}{2} N_4 N_4 \langle \sigma_{2\alpha} v \rangle\)のように書かれます。係数の\(1/2\)は、\(N_4\)から2つの\({}^4 \mathrm{He}\)を取り出す場合の数 \({}_{N_4} C_2\)からくるものです。こうしてできた\({}^8 \mathrm{Be}\)に、さらに\({}^4 \mathrm{He}\)が核融合を起こします。このときの反応断面積を\(\sigma_{2\alpha, \alpha}\)とすると、単位体積・単位時間あたりのトリプルアルファ反応数は

\[\frac{1}{2} N_4 N_4 \langle \sigma_{2\alpha} v\rangle \cdot N_4 \langle \sigma_{2\alpha, \alpha} v\rangle = \frac{N_4^3}{2} \langle 3\alpha \rangle\]

のように書くことができます。同様に、単位体積・単位時間あたりの\({}^{12} \mathrm{C} (\alpha, \gamma) {}^{16} \mathrm{O}, {}^{16} \mathrm{O} (\alpha, \gamma) {}^{20} \mathrm{Ne}\)の反応数はそれぞれ、\(N_4 N_{12} \langle \alpha 12\rangle, N_4 N_{16} \langle \alpha 16\rangle\)と書かれることから

\[\frac{dN_4}{dt} = - \frac{N_4^3}{2} \langle 3\alpha \rangle - N_4 N_{12} \langle \alpha 12 \rangle - N_4 N_{16} \langle \alpha 16 \rangle \tag{1}\] \[\frac{dN_{12}}{dt} = \frac{1}{3} \frac{N_4^3}{2} \langle 3\alpha \rangle - N_4 N_{12} \langle \alpha 12 \rangle \tag{2}\] \[\frac{dN_{16}}{dt} = N_4 N_{12} \langle \alpha 12 \rangle - N_4 N_{16} \langle \alpha 16 \rangle \tag{3}\] \[\frac{dN_{20}}{dt} = N_4 N_{16} \langle \alpha 16 \rangle \tag{4}\]

のようになります。 (2)式の\(1/3\)の係数は、トリプルアルファ反応で\({}^4 \mathrm{He}\)粒子が3つ消費され、\({}^{12} \mathrm{C}\)が1つ生成されることを表すものです。

質量比が満たす微分方程式

質量比は、その定義から

\[N_4 = \frac{\rho X_4}{4m_p}, \quad N_{12} = \frac{\rho X_{12}}{12m_p}, \quad N_{16} = \frac{\rho X_{16}}{16m_p}, \quad N_{20} = \frac{\rho X_{20}}{20m_p} \tag{5}\]

を満たします。そしてそれぞれの核融合反応によるエネルギー発生率が

\[\frac{N_4^3 \langle 3\alpha \rangle}{\rho} \simeq \frac{3!}{Q_{3\alpha}} \times 5.1 \times 10^8 \rho^2 X_4^3 \frac{e^{-4.4027/T_9}}{T_9^3} \equiv C_{3\alpha} (\rho, T_9) X_4^3 \tag{6}\] \[\frac{N_4 N_{12} \langle \alpha 12 \rangle}{\rho} \simeq \frac{1}{Q_{\alpha 12}} \times 10^{25} \frac{X_4 X_{12} \rho}{T_9^2} \exp \left\{ -\frac{32.12}{T_9^{1/3}} - (0.286 T_9)^2\right\} \equiv C_{\alpha 12} (\rho, T_9) X_4 X_{12} \tag{7}\] \[\frac{N_4 N_{16} \langle \alpha 16 \rangle}{\rho} \simeq \frac{1}{Q_{\alpha 16}} \times 6.7 \times 10^{26} \frac{X_4 X_{16} \rho}{T_9^{2/3}} \exp \left\{ -\frac{39.757}{T_9^{1/3}} - (0.631 T_9)^2\right\} \equiv C_{\alpha 16} (\rho, T_9) X_4 X_{16} \tag{8}\]

であることから、(1)-(4)式は

\[\frac{dX_4}{dt} = -4m_p \left( \frac{C_{3\alpha}}{2} X_4^3 + C_{\alpha 12} X_4 X_{12} + C_{\alpha 16} X_4 X_{16}\right) \tag{9}\] \[\frac{dX_{12}}{dt} = 12m_p \left( \frac{C_{3\alpha}}{6} X_4^3 - C_{\alpha 12} X_4 X_{12} \right) \tag{10}\] \[\frac{dX_{16}}{dt} = 16m_p \left( C_{\alpha 12} X_4 X_{12} - C_{\alpha 16} X_4 X_{16} \right) \tag{11}\] \[\frac{dX_{20}}{dt} = 20m_p C_{\alpha 16} X_4 X_{16} \tag{12}\]

のように整理されます。これらを\(\frac{d\mathbf{X}}{dt} = \mathbf{f} (t, \mathbf{X})\)のように考えれば、ルンゲ・クッタ法により数値積分をすることができます。先程の(1)-(4)式を数値積分するのでも構いませんが、質量比には

\[X_4 + X_{12} + X_{16} + X_{20} = 1 \tag{13}\]

の関係式があるため、数値積分が上手に方程式系を解けているかをチェックすることができます。
これらの核融合反応は、トリプルアルファ反応によって制御されていると見ることができます。 (9)-(12)式のすべての項に\(X_4\)が入っていることから、\({}^4 \mathrm{He}\)が無くなったときが、これらの核融合反応の終了時間と考えて良いでしょう。

数値積分のJulia言語実装とその計算結果

これを解くためのJulia言語での実装を、以下に示します。

using DifferentialEquations
using LaTeXStrings
using Plots

function helium!(du, u, p, t)
    rho = 1.0e+4
    T9 = 0.15
    mp = 1.673e-24
    MeV = 1.0e+6 * 1.602e-12
    Q3a = 7.275 * MeV 
    Qa12 = 7.162 * MeV
    Qa16 = 4.734 * MeV
    c3a = 30.6e+8 * rho^2 / Q3a * exp(-4.4027/T9) / T9^3
    ca12 = 1.0e+25 * rho / Qa12 * exp(-32.12/T9^(1/3)-(0.286*T9)^2) / T9^2
    ca16 = 6.7e+26 * rho / Qa16 * exp(-39.757/T9^(1/3)-(0.631*T9)^2) / T9^(2/3)
    du[1] = -4 * mp * (0.5*c3a*u[1]^3 + ca12*u[1]*u[2] + ca16*u[1]*u[3])
    du[2] = 12 * mp * (c3a*u[1]^3/6 - ca12*u[1]*u[2])
    du[3] = 16 * mp * (ca12*u[1]*u[2] - ca16*u[1]*u[3])
    du[4] = 20 * mp * ca16 * u[1] * u[3]
end

yr = pi * 10^7
u0 = [1.0; 0.0; 0.0; 0.0]
tspan = (0.0, 5.0e+7*yr)
prob = ODEProblem(helium!, u0, tspan)
sol = solve(prob)
plt = plot(sol.t/yr, sol', label=[L"X_4" L"X_{12}" L"X_{16}" L"X_{20}"], lw=3, 
            ylims=(1e-10, 1.0), yscale=:log10, xlims=(1e+2, 1e+8), xscale=:log10, 
            legend=:bottomleft, xlabel="t [yr]", ylabel="Mass fraction")
savefig(plt, "helium_burning.png")

そしてこれを解いた結果を下図に示します。

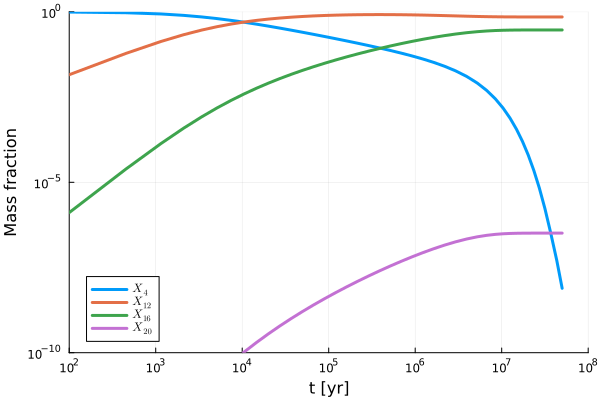
初期に\(X_4 = 1\)だったヘリウムは、炭素・酸素・ネオンを生成するのに使われることで、その量を減少させていきます。そして炭素・酸素が多く生成されていきます。炭素・酸素に続いてネオンも生成されるようになりますが、その前にヘリウムが枯渇を始めるため、ネオンの量はそこまで増加しません。簡単なモデルではありますが、ヘリウム燃焼による元素合成の様子を計算することができました。

参考文献

[1] Kippenhahn, Weigert & Weiss, “Stellar Structure and Evolution”
[2] 高原文郎, “宇宙物理学”
[3] 野本憲一, 定金晃三, 佐藤勝彦, “恒星”