Table of contents
球対称モデル
ここまで、分布関数について一般的に成り立つ式などを確認してきました。 ここでは球対称かつ時間に依存しない平衡状態について見ていきます。
球対称モデルで成り立つ式
基礎方程式
通常、空間座標は\(\mathbf{x} = (r, \theta, \varphi)\)の3次元ですが、球対称の場合は中心からの距離\(r\)のみを考慮すれば良いでしょう。 よって重力ポテンシャルなどは\(\Phi (r)\)のように書くことができます。 速度については\(\mathbf{v} = (v_r, v_\theta, v_\varphi)\)について考える必要があるのは変わりありません。 よってこの系の自由度は4つであることから、それに対応する運動の積分も4つとわかります。 具体的には系の全エネルギー\(E = \frac{1}{2} v^2 + \Phi\)と角運動量\(\mathbf{L} = \mathbf{x} \times \mathbf{v}\)の3成分です。 これらの議論とジーンズの定理より、分布関数は\(f(E, \mathbf{L})\)のように書けます。
さらに3次元曲座標系でのラプラシアンから、球対称の場合には
のようになります。よってポアソン方程式は
\[\frac{1}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial \Phi}{\partial r}\right) = 4\pi G \iiint f \left( E, \mathbf{L} \right) d\mathbf{v} \tag{2}\]となります。以下、さらに簡単化するために、分布関数はエネルギーのみに依存するとします。すなわち
\[f = f(E) = f\left( \frac{1}{2} v^2 + \Phi \right) \tag{3}\]として球対称モデルの分布関数を求めることとします。
分布関数がエネルギーにしか依存しない場合、これをエルゴード的(erodic)と呼びます。思い返してみると、学部で勉強する統計力学では分布関数がエネルギーにしか依存していませんね。
平均速度と速度分散
これまでの議論を踏まえて平均速度を求めましょう。そのためにまずは物理量\(A(\mathbf{x}, \mathbf{v})\)の平均を以下のように定義します。
\[\overline{A} (\mathbf{x}) = \frac{\iiint A(\mathbf{x}, \mathbf{v}) f(\mathbf{x}, \mathbf{v}) d\mathbf{v}}{\iiint f(\mathbf{x}, \mathbf{v}) d\mathbf{v}} = \frac{1}{\rho} \iiint A (\mathbf{x}, \mathbf{v}) f(\mathbf{x}, \mathbf{v}) d\mathbf{v} \tag{4}\]この定義に従い、まずは\(r\)成分から計算しましょう。 \(r\)方向の速度の取りうる範囲を\([-v_{r, 0}, v_{r, 0}]\)のように取り、対称区間で積分することを考えると
\[\overline{v}_r = \frac{1}{\rho} \iiint_{-v_{r, 0}}^{v_{r, 0}} v_r f\left( \frac{1}{2} (v_r^2 + v_\theta^2 + v_\varphi^2) + \Phi (r)\right) dv_r dv_\theta dv_\varphi \tag{5}\]関数の形から、\(f\)は\(v_r\)の偶関数です。そこに\(v_r\)がかけられているため、被積分関数は全体で奇関数となります。 それを対称区間で積分するので、結局この積分はゼロになります。\(v_\theta, v_\varphi\)方向についても同様に考えることができるため、
\[\overline{v}_r = \overline{v}_\theta = \overline{v}_\varphi = 0 \tag{6}\]のようになります。この平均を用いて、この系の速度分散は
\[\overline{(v_r - \overline{v}_r)^2} = \overline{v_r^2} = \frac{1}{\rho} \iiint v_r^2 f\left( \frac{1}{2} (v_r^2 + v_\theta^2 + v_\varphi^2) + \Phi (r) \right) dv_r dv_\theta dv_\varphi \tag{6}\]のように計算されます。さらに等方的という仮定を導入すると\(\overline{v_r^2} = \overline{v_\theta^2} = \overline{v_\varphi^2}\)のように、全ての方向で速度分散が等しくなります。
変数の再定義
(2)式を解きやすくするために、以下のエネルギー図を用いて変数変換を行いましょう。

重力多体系は有限の半径を持っているはずなので、粒子の分布もその半径以内に存在すると考えることができます。 すなわちある基準となる重力エネルギー\(\Phi_0\)よりも、その多体系に存在する粒子のエネルギーは低いと考えることができるでしょう。 よって粒子の存在範囲は\(E = \frac{1}{2} v^2 + \Phi \leq \Phi_0\)のように限定することができます。 このことから、以下のような常に正の値を取る変数を考えることができます。
\[\mathcal{E} \equiv \Phi_0 - E \geq 0 \tag{7}\] \[\Psi (r) \equiv \Phi_0 - \Phi \geq \frac{1}{2} v^2 \geq 0 \tag{8}\]これらを用いると、\(\mathcal{E} = \Psi (r) + \Phi - E = \Psi(r) - \frac{1}{2} v^2\)より
\[\frac{1}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial \Psi}{\partial r}\right) = - 4\pi G \iiint f \left( \Psi(r) - \frac{1}{2} v^2 \right) d\mathbf{v} \tag{9}\]これを計算すれば良いことがわかります。ここでは球対称系を考えているため、速度空間の3次元の積分は\(d\mathbf{v} = 4\pi v^2 dv\)のように考えることができます。 さらに積分範囲については、(8)式より
\[\frac{1}{2} v^2 \leq \Psi(r) \ \Longrightarrow \ 0 \leq v \leq \sqrt{2 \Psi(r)} \tag{10}\]のようになります。以上から
\[\frac{1}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial \Psi}{\partial r}\right) = - 16\pi^2 G \int_0^{\sqrt{2\Psi (r)}} v^2 f\left( \Psi(r) - \frac{1}{2} v^2 \right) dv \tag{11}\]と書くことができます。
ポリトロープ (polytrope)
その性質が良く調べられているものの一つにポリトロープ構造の場合が挙げられます。 これは分布関数が以下のように記述されるモデルです。
\[f(\mathcal{E}) = \left\{ \begin{array}{ll} F \mathcal{E}^{n-\frac{3}{2}} & (\mathcal{E} \geq 0) \\ 0 & (\mathcal{E} < 0) \end{array} \right. \tag{12}\]このとき、密度は
\[\rho (r) = 4\pi \int_0^\infty v^2 f(\mathcal{E}) dv = 4\pi F \int_0^\sqrt{2 \Psi} v^2 \left( \Psi - \frac{1}{2} v^2\right)^{n-\frac{3}{2}} dv \tag{13}\]を計算することで求めることができます。この積分を実行するために、\(v^2 = 2\Psi \cos^2 \theta\)のように変数変換を行いましょう。すると
\[\begin{align} \rho(r) &= 4\pi F \int_{\pi/2}^0 2\Psi (1-\sin^2 \theta) \Psi^{n-\frac{3}{2}} (1-\cos^2 \theta)^{n-\frac{3}{2}} \frac{- 2\Psi \sin \theta \cos \theta}{\sqrt{2\Psi} \cos \theta} d\theta \notag \\ &= 2^{\frac{7}{2}} \pi F \Psi^n \left( \int_0^{\pi/2} \sin^{2n-2} \theta d\theta - \int_0^{\frac{\pi}{2}} \sin^{2n} \theta d\theta \right) \tag{14} \end{align}\]ベータ関数を用いることで得られる\(\sin^n \theta\)の積分公式より
\[\int_0^{\pi/2} \sin^{2n} \theta d\theta = \frac{\sqrt{\pi}}{2} \frac{\Gamma \left( \frac{2n+1}{2}\right)}{\Gamma (n+1)}, \quad \int_0^{\pi/2} \sin^{2n-2} \theta d\theta = \frac{\sqrt{\pi}}{2} \frac{\Gamma \left( \frac{2n-1}{2}\right)}{\Gamma (n)} \tag{15}\]を用いると
\[\begin{align} \rho(r) &= 2^{7/2} \pi F \Psi^n \frac{\sqrt{\pi}}{2} \left( \frac{\Gamma \left( \frac{2n-1}{2}\right)}{\Gamma(n)} - \frac{\frac{2n-1}{2} \Gamma \left( \frac{2n-1}{2}\right)}{n \Gamma(n)}\right) = 2^{5/2} \pi^{3/2} F \Psi^n \frac{\Gamma \left( \frac{2n-1}{2}\right)}{\Gamma (n)} \frac{1}{2n} \notag \\ &= \underbrace{(2\pi)^{3/2} F \frac{\left( n-\frac{3}{2}\right)!}{n!}}_{\equiv c_n} \Psi^n \tag{16} \end{align}\]のように求まります。\(\Gamma\)関数の性質より\(c_n\)が有限になるには、\(n>1/2\)であることもわかります。 (16)式を用いると、(11)式は
\[\frac{1}{r^2} \frac{d}{dr} \left( r^2 \frac{d\Psi}{dr}\right) + 4\pi G c_n \Psi^n = 0 \tag{17}\]のように書かれることがわかります。 ここで\(s = r/ b, \psi = \Psi/ \Psi_0\)のような変数変換を施します。 ここで\(\Psi_0 \equiv \Psi(0), b \equiv (4\pi G \Psi_0^{n-1} c_n)^{-1/2}\)です。すると
\[\frac{1}{s^2} \frac{d}{ds} \left( s^2 \frac{d \psi}{ds}\right) + \psi^n = 0 \tag{18}\]という方程式が得られます。これをレーン・エムデン方程式 (Lane-Emden equation)と呼びます。 この方程式を解くことで\(\psi\)が求まり、そこから\(\Psi\)そして\(\rho\)が求まります。
一般の\(n\)に対して、この方程式を解析的に解くことはできません。よって数値的にこの微分方程式を解く必要があります。 \(\psi = \Psi / \Psi_0\)の定義より、\(s = 0\)で\(\psi = 1\)です。 さらに中心部でその勾配がゼロ、すなわち\(\frac{d\psi}{ds} = 0\)のような初期条件を用いることで、ルンゲ・クッタ法などで数値的に解くことができます。 数値的に解いていくと、あるところで\(\psi < 0\)となる点が出現します。しかし\(\psi\)の定義から、これは必ず正の値でなければなりません。 言い換えると、下図のように\(\psi \geq 0\)の部分はこの系の存在する範囲を表しており、\(\psi = 0\)となる部分がこの重力多体系の半径と言えます。 以下、この値を\(s_1\)と書くことにします。

\(n = 0\)
一般の\(n\)では解析的に解くことは難しいですが、以下に示すように\(n=0, 1, 5\)であれば解析的な解を求めることが可能です。 まずは\(n=0\)の場合です。(18)式より
\[\frac{d}{ds} \left( s^2 \frac{d\psi}{ds}\right) = - s^2 \ \Longrightarrow \ s^2 \frac{d\psi}{ds} = -\frac{1}{3} s^3 + C_1 \tag{19}\]\(s = 0\)で左辺がゼロになることから、積分定数\(C_1\)もゼロとなります。よって
\[\frac{d\psi}{ds} = - \frac{1}{3} s \ \Longrightarrow \ \psi = - \frac{1}{6} s^2 + C_2 \tag{20}\]\(s = 0\)で\(\psi = 1\)より
\[\psi = 1 -\frac{1}{6} s^2 \tag{21}\]となります。\(\psi = 0\)となるのは\(s_1 = \sqrt{6}\)と求まります。
\(n = 1\)
この方程式の解は
\[\psi = \frac{\sin s}{s} \tag{22}\]と求まります。一応確認だけしておきましょう。
\[\frac{d\psi}{ds} = \frac{s \cos s - \sin s}{s^2} \ \Longrightarrow \ \frac{d}{ds} \left( s^2 \frac{d\psi}{ds} \right) = - s \sin s \ \Longrightarrow \ \frac{1}{s^2} \frac{d}{ds} \left( s^2 \frac{d \psi}{ds} \right) = - \psi\]となり、確かに(18)式で\(n=1\)のときの解になっていることがわかります。 このとき\(\psi = 0\)となる値は\(s_1 = \pi\)と求まります。
プラマーモデル (Plummer model)
最後は\(n=5\)の場合です。このときの解は
\[\psi = \frac{1}{\sqrt{1+\frac{1}{3} s^2}} \tag{23}\]であることが知られています。これも確認してみましょう。
\[\begin{align} &\frac{d\psi}{ds} = - \frac{1}{3} s \left( 1+\frac{1}{3} s^2\right)^{-3/2} \ \Longrightarrow \ \frac{d}{ds} \left( s^2 \frac{d \psi}{ds}\right) = - s^2 \left( 1+\frac{1}{3} s^2\right)^{5/2} \notag \\ &\Longrightarrow \ \frac{1}{s^2} \frac{d}{ds} \left( s^2 \frac{d\psi}{ds} \right) = - \psi^5 \end{align}\]となり、\(n=5\)のときの(18)式を満たしています。 (23)式をみればわかるように、\(\psi\)は\(s \rightarrow \infty\)でようやくゼロに近づきます。 このことから、\(s_1 = \infty\)、すなわちこの重力多体系の半径は無限大であることがわかります。 半径は無限大ですが、実は系の全質量\(M\)は有限の値になることが知られています。ポアソン方程式より
\[M = \int_0^\infty 4\pi r^2 \rho(r) dr = \frac{1}{G} \int_0^\infty \frac{d}{dr} \left( \frac{d\Phi}{dr} \right) dr = \frac{1}{G} \left( r^2 \frac{d\Phi}{dr} \right)_{r \rightarrow \infty} \tag{24}\]右辺を\(s = r /b, \Psi = \Phi_0 - \Phi\)を用いて表すと
\[M = - \frac{b}{G} \left( s^2 \frac{d\Psi}{ds}\right)_{s \rightarrow \infty} \tag{25}\]さらに(23)式から
\[\Psi = \Psi_0 \psi = \Psi_0 \left( 1+\frac{1}{3} s^2\right)^{-1/2} \tag{26}\]を用いると
\[M = \frac{b \Psi_0}{3 G} \left( \frac{s^3}{\left( 1+\frac{1}{3} s^2 \right)^{3/2}} \right)_{s \rightarrow \infty} = \frac{\sqrt{3} b \Psi_0}{G} \tag{27}\]のように求まります。(16)式からもわかるように、密度は
\[\rho(r) = c_5 \Psi^5 = c_5 \Psi_0^5 \psi^5 \propto \left( 1+\frac{1}{3} s^2\right)^{-5/2}\tag{28}\]のような\(s\)依存性です。 密度が\(s = 0\)で有限かつ\(s \rightarrow \infty\)で\(1/s^3\)よりも素早くゼロに減衰するため、有限の質量となります。
実は、このようなモデルには名前がついています。1911年にプラマー(Plummer)が提案したことから、プラマーモデルと呼ばれています。 実際には以下のようなものです。
プラマーはこの球対称ポテンシャルと密度を用いて、球状星団の観測にフィットする研究を行いました。 このモデルは球状星団の進化をシミュレーションする初期条件として用いられます。
等温モデル (isothermal model)
特異な等温モデル (singular isothermal model)
ここまで、特にこの重力多体系は熱平衡状態かどうかは議論してきませんでした。 もしこの系がある温度で一様であるとして、また熱平衡状態にあるとします。 ここで重力多体系の温度そして圧力は、その重力多体系を構成する粒子(例えば恒星など)の速度などから、重力に逆らう物理量を意味するものとして考えることができます。 重力多体系を構成する粒子が速度を持って系内を運動することで、その重力多体系は潰れずにその形を保っているのです。 よってその多体系内の圧力を\(P(r)\)のように書くと、もしこの多体系が一定温度で熱平衡状態に落ち着いているならば、静水圧平衡の式より
\[\frac{dP}{dr} = - \rho \frac{d\Phi}{dr} \tag{30}\]が成り立ちます。さらにこの多体系内では一様温度であることから、状態方程式は
\[P = n k_B T = \frac{\rho}{m} k_B T \tag{31}\]と書くことができます。ここで、この重力多体系を構成する粒子の質量を全て等しく\(m\)としました。 この2式より
\[\frac{k_B T}{m} \frac{d\rho}{dr} = - \rho \frac{d\Phi}{dr} \underbrace{=}_{球対称系より} - \rho \frac{GM (r)}{r^2} \tag{32}\]となります。ここで\(M(r)\)は半径\(r\)の位置より内側に存在する質量です。両辺を整理すると
\[\frac{r^2}{\rho} \frac{d\rho}{dr} = r^2 \frac{d \ln \rho}{dr} = - \frac{Gm}{k_B T} M(r) \ \underbrace{\Longrightarrow}_{両辺r微分} \ \frac{d}{dr} \left( r^2 \frac{d \ln \rho}{dr} \right) = - \frac{Gm}{k_B T} \frac{dM}{dr} = - \frac{4\pi Gm}{k_B T} r^2 \rho \tag{33}\]と求まります。途中、\(\frac{dM}{dr} = 4\pi r^2 \rho\)を用いました。
ここで熱・統計力学の知識を応用しましょう。 もし系が熱平衡状態にあるならば、その分布関数はマクスウェル・ボルツマン分布で書かれるはずです。よって
の形を仮定します。これを速度について積分し、密度を求めてみると
\[\rho = \iiint f \left( \Psi - \frac{1}{2} v^2 \right) d\mathbf{v} = \frac{\rho_1 e^{\Psi/\sigma^2}}{(2\pi \sigma^2)^{3/2}} \int_0^\infty e^{-\frac{v^2}{2\sigma^2}} 4\pi v^2 dv = \rho_1 e^{\Psi/\sigma^2} \tag{35}\]のようになります。ここで球対称系を仮定していることから、全速度領域での体積積分は\(d\mathbf{v} = 4\pi v^2 dv \ (v^2 = v_r^2 + v_\theta^2 + v_\varphi^2)\)のようにしました。 これを\(r\)で微分したものは
\[\frac{d\rho}{dr} = \rho_1 e^{\Psi/\sigma^2} \frac{1}{\sigma^2} \frac{d\Psi}{dr} = \frac{\rho}{\sigma^2} \frac{d\Psi}{dr} \tag{36}\]です。これをポアソン方程式に代入すると
\[\frac{1}{r^2} \frac{d}{dr} \left( r^2 \frac{\sigma^2}{\rho} \frac{d\rho}{dr} \right) = - 4\pi G \rho \ \Longrightarrow \ \frac{d}{dr} \left( r^2 \frac{d \ln \rho}{dr} \right) = - \frac{4\pi G}{\sigma^2} r^2 \rho \tag{37}\]のように、(33)式と同じ形の式を得ます。 (33), (37)式の比較から
\[\sigma^2 = \frac{k_B T}{m} \tag{38}\]とわかります。多体系を構成する質量\(m\)が小さいほど、また多体系の温度\(T\)が高いほど、速度分散\(\sigma\)が大きな系に対応することがわかります。 では実際に、(37)式で与えられるこの系の密度はどのような関数をしているでしょうか。ひとまず\(\rho = C r^{-b}\)というべき乗の形で解を求めてみましょう。 すると
\[-b = - \frac{4\pi G}{\sigma^2} r^2 C r^{-b}\]左辺は\(r\)依存性が存在しないため、\(b = 2\)と求まります。ここから
\[C = \frac{\sigma^2}{2\pi G}\]となります。最終的に
\[\rho(r) = \frac{\sigma^2}{2\pi G r^2} \tag{39}\]を得ます。(39)式は\(r \rightarrow 0\)で密度が発散します。 またこのときの半径\(r\)内に含まれる全質量を求め、最後に\(r \rightarrow \infty\)としてみましょう。
\[M(r) = \int_0^r 4\pi r'^2 \rho(r') dr' = \frac{2 \sigma^2}{G} r \xrightarrow{r \rightarrow \infty} \infty \tag{40}\]このことから、このモデルは全質量が無限大に発散するモデルでもあることがわかります。 これを特異な等温モデルと呼びます。 「\(r=0\)での密度や全質量が発散したり、解析的には求まるけどあまり意味のないモデルなのでは?」と思われるかも知れません。 しかしこのモデルは、例えば楕円銀河の中心部や銀河ハローの中心部を、比較的良く近似できるものもあるということが知られています。 渦巻き銀河では回転速度が中心からの距離にほぼ依存せず一定になっている(\(v_c = 一定\))、という観測事実が存在します。 このとき、遠心力と重力の釣り合い、そして銀河の質量分布が球対称であると近似すると
\[\rho \frac{v_c^2}{r} = \rho \frac{GM(r)}{r^2} = \frac{\rho G}{r^2} \frac{4\pi}{3} r^3 \rho \ \Longrightarrow \ \rho \propto r^{-2} \tag{41}\]のようになります。このことからもわかるように、この等温モデルが重要であることがわかります。
キングモデル (King model)
等温の分布関数(34)式で全質量が発散する本質的な理由は、分布関数がエネルギー無限大(\(\mathcal{E} \rightarrow - \infty\))までゼロにならないことです。 本来ならば(7)式の定義から、\(\mathcal{E} \leq 0\)で\(f (\mathcal{E})= 0\)でなければなりませんが、このモデルはそうはなっていません。 これは全エネルギー\(E\)が負でないような粒子も存在することを意味します。 有限の質量のものが自己重力でまとまっているためには、全ての粒子のエネルギーが負でなければならないため、このモデルでは自己重力系をきちんと説明することはできないのです。 ここから、ある有限エネルギー以上のものは無くしてしまうようにモデルの改良を行えば、有限質量の等温モデルを構築することが可能であるとわかります。 よって、ここでは以下のように改良を加えたものを考えましょう。
\[f(\mathcal{E}) = \left\{ \begin{array}{ll} \frac{\rho_1}{(2\pi \sigma^2)^{3/2}} (e^{\mathcal{E}/\sigma^2} - 1) & (\mathcal{E} > 0) \\ 0 & (\mathcal{E} \leq 0) \end{array} \right. \tag{42}\]このモデルでは\(\mathcal{E} = 0\)で\(f = 0\)となります。 このモデルをキングモデルと呼び、これは球状星団のモデルとしてよく知られています。 具体的にどのような分布をしているのかを求めてみましょう。
\[\rho (\Psi) = \iiint f(\mathcal{E}) d\mathbf{v} = \frac{\rho_1}{(2\pi \sigma^2)^{3/2}} \int_0^{\sqrt{2\Psi}} \left\{ e^{\frac{\Psi - v^2 / 2}{\sigma^2}} -1 \right\} 4\pi v^2dv \tag{43}\]第一項の積分を計算すると
\[\begin{align} (第一項) &= 4\pi e^{\Psi/\sigma^2} \int_0^{\sqrt{2\Psi}} v \cdot v e^{-v^2 / 2\sigma^2} \underbrace{=}_{部分積分} 4\pi e^{\Psi/\sigma^2} \left\{ \left[ - v \sigma^2 e^{-v^2 / 2 \sigma^2} \right]_0^{\sqrt{2\Psi}} - \int_0^{\sqrt{2\Psi}} (-\sigma^2) e^{-v^2 / 2 \sigma^2} dv\right\} \notag \\ &= 4\pi e^{\Psi/\sigma^2} \left\{ - \sqrt{2\Psi} \sigma^2 e^{-\Psi / \sigma^2} + \sigma^2 \int_0^{\sqrt{2\Psi}} e^{-v^2 / 2 \sigma^2} dv \right\} \notag \\ &= -4 \pi \sqrt{2\Psi} \sigma^2 + 2\sqrt{2} \pi^{3/2} \sigma^3 e^{\Psi / \sigma^2} \mathrm{erf} (\sqrt{\Psi}/ \sigma) \tag{44} \end{align}\]のようになります。 ここで誤差関数
\[\mathrm{erf} (x) = \frac{2}{\sqrt{\pi}} \int_0^x e^{-t^2} dt \tag{45}\]を用いました。 続いて第二項は
\[(第二項) = 4\pi \int_0^\sqrt{2\Psi} v^2 dv = \frac{4\pi}{3} (2\Psi)^{3/2} \tag{46}\]のように計算されるので、これらを合わせて
\[\rho (\Psi) = \rho_1 \left\{ e^{\Psi/\sigma^2} \mathrm{erf} ( \sqrt{\Psi} / \sigma) - \sqrt{\frac{4\Psi}{\pi \sigma^2}} \left( 1 + \frac{2\Psi}{3 \sigma^2}\right) \right\} \tag{47}\]を得ます。 このようにして密度がポテンシャルの関数として求まったため、これをポアソン方程式に代入すればポテンシャルが求まります。 すると
\[\frac{d}{dr} \left( r^2 \frac{d\Psi}{dr}\right) = - 4\pi G \rho_1 r^2 \left\{ e^{\Psi/\sigma^2} \mathrm{erf} ( \sqrt{\Psi} / \sigma) - \sqrt{\frac{4\Psi}{\pi \sigma^2}} \left( 1 + \frac{2\Psi}{3 \sigma^2}\right) \right\} \tag{48}\]この微分方程式は解析的には解けないため、数値的に求める必要があります。 このとき、数値積分は\(r = 0\)から出発し、境界条件として\(\frac{d\Psi}{dr} = 0\)と\(\Psi(0)\)に適当な値を選びます。 こうして\(\Psi(r)\)を得ることができます。 \(\Psi\)は定義式(8)から、基準となる重力エネルギーからポテンシャルエネルギーを差し引いたものです。 よって\(r\)が大きくなるにつれてその値は減少し、ついにはあるところでゼロとなることが考えられます。 この半径を\(r_t\)としましょう。 このとき、実は\(\Psi(r_t) = 0\)となるだけでなく、(47)式から\(\rho(\Psi(r_t)) = 0\)となることもわかります。 \(r > r_t\)では\(\Psi < 0\)となるため、\(r_t\)より外側の領域では\(\mathcal{E} = \Psi (r) - \frac{1}{2} v^2 \leq 0\)となります。 すると(42)式から\(f(\mathcal{E}) =0\)であるため、\(r > r_t\)では\(\rho = 0\)であることがわかります。 この\(r_t\)を、キングモデルの潮汐半径(tidal radius)と呼びます。 今、基準となる重力エネルギーを\(\Phi (r_t)\)に選ぶと、ポテンシャルは\(\Phi = \Phi(r_t) - \Psi\)のように書かれます。 実は\(\Phi (r_t)\)は
\[\Phi (r_t) = - \frac{GM(r_t)}{r_t} \quad \left( M = 4\pi \int_0^{r_t} r^2 \rho (r) dr\right) \tag{49}\]のように計算することができます。 ここで\(M\)は\(r<r_t\)内に存在する質量、すなわち全質量を表します。 これより
\[\Phi (0) = - \frac{GM}{r_t} - \Psi (0) \tag{50}\]と求まります。 さきほど「境界条件として\(\Psi(0)\)を適当に選ぶ」と記述しましたが、この関係式から\(\Psi (0)\)を大きくすると\(\vert \Phi (0) \vert\)が大きくなります。 中心部での重力ポテンシャルが深くなるため、これは\(M\)、そして\(r_t\)が大きくなることを意味します。
潮汐半径\(r_t\)とは別に、キングモデルの典型的な半径として、以下のキング半径があります。
ここで\(\rho_0\)は(47)式を数値的に解くことで得られた中心の密度を表します。 潮汐半径とキング半径の比の対数
\[c \equiv \log_{10} (r_t/ r_0) \tag{52}\]を、concentration (集中度?)と呼びます。 実際の研究で観測データにキングモデルを適用した場合の論文などでは、これをパラメータとして記述することが多いようです。
Isochroneポテンシャルモデル
以下のような重力ポテンシャルで与えられるモデルを、isochroneポテンシャルと呼びます。
\[\Phi (r) = - \frac{GM}{b + \sqrt{b^2 + r^2}} \tag{53}\]これは質点が作るポテンシャル\(\Phi_\mathrm{point}= - \frac{GM}{r}\)を、\(b\)だけスムージングしたものです。 当然、\(b \rightarrow 0\)または\(r \gg b\)では、質点が作るポテンシャルに漸近します。
このポテンシャルモデルがどれだけ速く質点のポテンシャルに漸近するかを、\(b/r\)で展開することで見てみましょう。
第一項は質点が作る重力ポテンシャルです。 第二項は\(r^{-2}\)に比例する項であることがわかります。 ポアソン方程式より、密度分布を計算しましょう。
\[\frac{1}{r^2} \frac{\partial}{\partial r} \left( r^2 \frac{\partial \Phi_\mathrm{other}}{\partial r}\right) = \frac{2GMb}{r^4} = 4\pi_{r \gg b} G \rho \ \Longrightarrow \ \rho = \frac{Mb}{2 \pi r^4} \tag{55}\]この\(\rho_{r \gg b} \propto r^{-4}\)は、ダークマターハローのモデルであるハーンキストモデルの振る舞いと同じです。
次に\(r/b \rightarrow 0\)の場合を考えましょう。
再びポアソン方程式より
\[4\pi G \rho = \frac{6GM}{8b^3} \ \Longrightarrow \ \rho = \frac{3M}{16\pi b^3} \tag{57}\]と求まります。 このことから、isochroneポテンシャルが作る質量分布は、中心部では一定密度となることがわかります。 以上の議論から、このポテンシャルモデルは質点が作るポテンシャルと、一定密度分布が作るポテンシャルとをなめらかに繋ぐポテンシャルであることがわかります。
次に、このポテンシャル中を円運動する粒子の運動速度を計算しましょう。 遠心力と重力との釣り合いより
となります。 このモデルが最も注目される理由としては、すべての軌道を解析的に解くことができる、最も現実的な銀河のモデルとなっているためです。 解析的に解けるトイモデルというのは、それだけで魅力的なのです。
べき乗則モデル (Power-law models)
もう一つの重要なモデルとして、半径\(r\)に対して質量密度がべき乗分布するものがあります。
\[\rho (r) = \rho_0 \left( \frac{r_0}{r} \right)^\alpha \tag{59}\]ここで\(\rho_0\)は\(r=r_0\)における質量密度を表します。 半径\(r\)以内に存在する総質量を計算しましょう。
\[M (r) = 4\pi \int_0^r \rho_0 \left( \frac{r_0}{r} \right)^\alpha r^2 dr = 4\pi \rho_0 r_0^\alpha \int_0^r r^{2-\alpha} dr = \frac{4\pi \rho_0 r_0^3}{3-\alpha} \left( \frac{r_0}{r} \right)^{\alpha -3} \tag{60}\]質量\(M(r)\)は正であるため、\(\alpha < 3\)を仮定しました。 半径\(r\)における回転速度は
\[\frac{v_c^2}{r} = \frac{GM}{r^2} = \frac{4\pi G \rho_0 r_0^\alpha}{3-\alpha} r^{1-\alpha} \ \Longrightarrow \ v_c^2 = \frac{4\pi G \rho_0 r_0^\alpha}{3-\alpha} r^{2-\alpha} \tag{61}\]のように求まります。 ここまで、\(\alpha\)が実際にどのような値かは議論してきませんでした。 実際の円盤銀河では、中心部から離れると\(v_c = 一定\)のflat rotationであることが知られています。 それを再現するには、(61)式で\(\alpha = 2\)であれば良いとわかります。 その場合、重力ポテンシャルは
\[\Phi(r) - \Phi (r_0) = G \int_{r_0}^r \frac{M(r')}{r'^2} dr' = 4\pi G \rho_0 r_0^2 \int_{r_0}^r \frac{dr'}{r'} = 4\pi G \rho_0 r_0^2 \ln (r/r_0) = v_c^2 \ln (r/r_0) \tag{62}\]のように求まります。 ここで\(r_0\)をポテンシャルの基準とし、さらに\(\alpha = 2\)のとき\(v_c^2 = 4\pi G \rho_0 r_0^2\)であることを用いました。 このポテンシャルはlogarithmic potential (対数ポテンシャル) と呼ばれ、銀河のflat rotationを再現する重要なポテンシャルです。
2つのべき乗を用いた密度モデル (Two-power density models)
もう一つ重要なモデルとして、以下のような質量密度のものがあります。
\[\rho (r) = \frac{\rho_0}{\left( \frac{r}{a} \right)^\alpha \left( 1+\frac{r}{a} \right)^{\beta - \alpha}} \tag{63}\]ここで\(a\)は適当な定数です。 このモデルは
\[\rho(r) \approx \left\{ \begin{array}{ll}\rho_0 \left( \frac{a}{r}\right)^\alpha & (r \ll a) \\ \rho_0 \left(\frac{a}{r}\right)^\beta & (r \gg a) \end{array} \right. \tag{64}\]のように表現され、\(r \sim a\)付近でそのべきが\(\alpha \rightarrow \beta\)に変化します。 このような理由から、定数\(a\)をスケール半径と呼びます。 このモデルを一般の\(\alpha, \beta\)について議論すると大変なため、ここでは\((\alpha, \beta) = (1, 4), (2, 4), (1, 3)\)の場合のみ議論しましょう。 特に\((\alpha, \beta) = (1, 4)\)をハーンキストモデル (Hernquist model)、\((\alpha, \beta) = (2, 4)\)をジャッフェモデル (Jaffe model)、そして\((\alpha, \beta) = (1, 3)\)をNFWモデルと呼びます。
半径\(r\)内に存在する質量は
のようになります。 では\((\alpha, \beta) = (1, 4)\)から順に求めていきましょう。
\[\begin{align} M(r) &= 4\pi \rho_0 a^3 \int_0^{r/a} \frac{s}{(1+s)^3} ds = 4\pi \rho_0 a^3 \left( \left[ -\frac{1}{2} s (1+s)^{-2}\right]_0^{r/a} + \frac{1}{2} \int_0^{r/a} (1+s)^{-2} ds \right) \notag \\ &= 4\pi \rho_0 a^3 \left\{ - \frac{r}{2a (1+r/a)^2} + \frac{1}{2} \left[ -(1+s)^{-1} \right]_0^{r/a}\right\} \notag \\ &= 4\pi \rho_0 a^3 \left\{ - \frac{r}{2a (1+r/a)^2} - \frac{1}{2} \left( \frac{1}{1+r/a} -1\right) \right\} = 4\pi \rho_0 a^3 \frac{ \left( \frac{r}{a} \right)^2}{2 \left( 1 + \frac{r}{a} \right)^2} \tag{66} \end{align}\]続いて\((\alpha, \beta) = (2, 4)\)の場合です。
\[\begin{align} M(r) &= 4\pi \rho_0 a^3 \int_0^{r/a} (1+s)^{-2} ds = 4\pi \rho_0 a^3 \left[ -(1+s)^{-1}\right]_0^{r/a} = 4\pi \rho_0 a^3 \left( 1-\frac{1}{1+\frac{r}{a}}\right) \notag \\ &= 4\pi \rho_0 a^3 \frac{\frac{r}{a}}{1+\frac{r}{a}} \tag{67} \end{align}\]そして\((\alpha, \beta) = (1, 3)\)の場合は
\[\begin{align} M(r) &= 4\pi \rho_0 a^3 \int_0^{r/a} \frac{s}{(1+s)^2} ds = 4\pi \rho_0 a^3 \left\{ \left[ -(1+s)^{-1} s\right]_0^{r/a} + \int_0^{r/a} (1+s)^{-1} ds \right\} \notag \\ &= 4\pi \rho_0 a^3 \left\{ - \frac{\frac{r}{a}}{1+\frac{r}{a}} + \left[ \ln (1+s)\right]_0^{r/a} \right\} = 4\pi \rho_0 a^3 \left\{ \ln \left( 1+\frac{r}{a} \right) - \frac{\frac{r}{a}}{1+\frac{r}{a}} \right\} \tag{68} \end{align}\]のようになります。 以上から
\[M(r) = 4\pi \rho_0 a^3 \times \left\{ \begin{array}{ll} \frac{(r/a)^2}{2(1+r/a)^2} & (\mathrm{Hernquist}) \\ \frac{r/a}{1+r/a} & (\mathrm{Jaffe})\\ \ln (1+r/a) - \frac{r/a}{1+r/a} & (\mathrm{NFW}) \end{array} \right. \tag{69}\]のようにまとめることができます。 ハーンキストモデルの場合、\(r \rightarrow \infty\)で\(M = 2\pi \rho_0 a^3\)となります。 ジャッフェモデルでは\(r \rightarrow \infty\)で\(M=4\pi \rho_0 a^3\)です。 すなわちこれらのモデルでは、これが全系の質量となります。 しかしNFWモデルでは、\(r \rightarrow \infty\)で質量が無限大に発散します。 そのため、NFWモデルを実際の銀河に適用する場合には、有限の半径までを銀河の系としなければなりません。
続いて、重力ポテンシャルを求めてみましょう。 まずは\((\alpha, \beta) = (1, 4)\)の場合です。
次は\((\alpha, \beta) = (2, 4)\)についてです。
\[\begin{align} \Phi(r) &= - G \int_r^\infty \frac{dr'}{r'^2} 4\pi \rho_0 a^3 \frac{r'/a}{1+r'/a} = - 4\pi G \rho_0 a^2 \int_r^\infty \frac{1}{r'} \frac{1}{1+r'/a} dr' \notag \\ &= - 4\pi G \rho_0 a^2 \int_r^\infty \left( \frac{1}{r'} - \frac{1}{a} \frac{1}{1+r'/a} \right) dr' = - 4\pi G \rho_0 a^2 \left[ \ln r' - \ln \left(1+ \frac{r'}{a} \right) \right]_r^\infty \notag \\ &= - 4\pi G \rho_0 a^2 \ln \left(1+\frac{a}{r} \right) \tag{71} \end{align}\]最後に、\((\alpha, \beta) = (1, 3)\)です。
\[\begin{align} \Phi(r) &= -G \int_r^\infty \frac{dr'}{r'^2} 4\pi \rho_0 a^3 \left\{ \ln (1+r'/a) - \frac{r'/a}{1+r'/a}\right\} = -4\pi G \rho_0 a^3 \left\{ \int_r^\infty \frac{dr'}{r'^2} \ln (1+r'/a) -\int_r^\infty \frac{dr'}{r'^2} \frac{r'/a}{1+r'/a} \right\} \notag \\ &= - 4\pi G \rho_0 a^3 \left\{ \left[ - r^{-1} \ln (1+r'/a)\right]_r^\infty + \int_r^\infty r^{-1} \frac{1/a}{1+r'/a} dr' -\int_r^\infty \frac{dr'}{r'^2} \frac{r'/a}{1+r'/a} \right\} \notag \\ &= -4\pi G \rho_0 a^2 \frac{a}{r} \ln \left( 1 + \frac{a}{r} \right) \tag{72} \end{align}\]以上をまとめると
\[\Phi (r) = - 4 \pi G \rho_0 a^2 \times \left\{ \begin{array}{ll} \frac{1}{2(1+r/a)} & (\mathrm{Hernquist}) \\ \ln (1+a/r) & (\mathrm{Jaffe}) \\ \frac{a}{r} \ln (1+a/r) & (\mathrm{NFW}) \end{array} \right. \tag{73}\]ハーンキストモデルでは、全質量が\(M_\mathrm{Hernquist} = 2\pi \rho_0 a^3\)となるのでした。 ここから、ハーンキストモデルにおける重力ポテンシャルは
\[\Phi_\mathrm{Hernquist} (r) = - \frac{GM}{r+a} \tag{74}\]のように書き直すことができます。 すなわちハーンキストモデルの重力ポテンシャルは、質点のポテンシャルを\(r \rightarrow r +a\)としたものに等しいことがわかります。 ハーンキストモデルは楕円銀河の\(r^{1/4}\)のドゥ・ボクルール則 (de Vaucouleurs sourface-brightness profile)を再現することから、楕円銀河や銀河のバルジ部分のモデルとして有名です。
これに対してジャッフェモデルは、とてもカスピー (cuspy、中心部で質量密度がとても大きくなるような分布)なものとして知られています。 これはもちろん現実の銀河ハローなどとは異なりますが、ジャッフェモデルは解析的に扱いやすいという利点があり、広く用いられています。
NFWモデルは、Navarro et al. (1996, 1997)で示されたモデルです。 これは宇宙論的なN体計算から求められた、冷たいダークマターハローの質量密度分布モデルです。 Navarroたちは、様々な宇宙初期の密度ゆらぎからダークマターのみのN体計算を行いました。 そしてどのような初期条件からシミュレーションを開始しても、普遍的にこの質量密度分布になることを見出したのです。 しかし、どのような物理機構でこの分布が再現されるのかについては決着がついていません。 また最近のより高精度な数値シミュレーションでは、ダークマターハローの中心部の密度分布は、必ずしもNFW分布にならないことが知られています。 さらにダークマターハロー外縁部についても、これを良く再現する分布は得られていません。 種々の研究から、NFWよりハーンキストモデルに近い質量密度分布であると言われています。
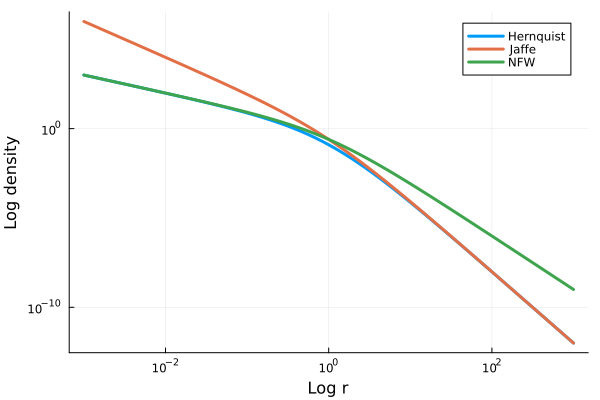
下図はハーンキスト・ジャッフェ・NFWモデルの質量密度分布を図示したものです。
NFW分布とコア・カスプ問題
普遍的に成り立つNFW分布ですが、実は矮小銀河などの低質量銀河ではこれとは異なる分布を持つことが知られています。 観測から判明している矮小銀河の中心の質量分布は、ほぼ一定のコア構造になっているのです。 一方、NFW分布では、中心部の質量分布はカスピーなものになります。 このような食い違いをコア・カスプ問題 (core-cusp problem)と呼ばれています。
この問題を解決する手段として、以下の2つが挙げられます。
- バリオンの物理を考慮する (stellar feedbacks, tidal force, reionization etc.)
銀河中心領域での星形成そして形成された恒星の超新星爆発を考慮することでや、銀河中心にできる超大質量ブラックホールのAGN活動により、これを軽減することができるとされています。 超新星爆発などにより中心部からガスが吹き飛ばされると、重力相互作用をするダークマターもまた、そのガスに引っ張られる形で周辺部へ移動します。 結果として、中心部に一極集中するはずだったダークマターが、その周りにも分布するようになるという説です。
- 冷たいダークマター以外のダークマター理論 (WDM, SIDM, FDM etc.)
ダークマターの候補となっているものは様々提案されており、それらがこの問題を解決するのではないか、という説です。 有名なものとしては、冷たいダークマターよりも速度分散が大きい温かいダークマター (Warm Dark Matter: WDM)、冷たいダークマターよりも強い自己相互作用を持つ自己相互作用ダークマター (Self-Interacting Dark Matter: SIDM)、とても軽い質量のスカラー粒子からなるファジーダークマター (Fuzzy Dark Matter: FDM)などが挙げられます。 これらダークマターは、そのダークマター自身の性質により小さいスケールでの構造を抑制し、コア構造を形成することが可能とされています。 逆を言えば、矮小銀河の構造から乱立するダークマター理論に対して制限をかけることも可能です。 天の川銀河の周辺に存在する矮小銀河だけを見ても、まだまだ謎が多く、次世代の観測に期待が寄せられています。
参考文献
[1] Binney & Tremaine, “Galactic Dynamics: Second Edition”
[2] Bovy, “Dyanmics and Astrophysics of Galxies”
[3] 牧野淳一郎, “理論天体物理学特論I”
[4] 谷口義明, 岡村定矩, 祖父江義明, “銀河 I”
[5] 観山正見, 野本憲一, 二間瀬敏史, “天体物理学の基礎 II”
[6] Navarro et al., 1996, “The Structure of Cold Dark Matter Halos”
[7] Navarro et al., 1997, “A Universal Density Profile from Hierarchical Clustering”
[8] 林航平, “2020年度 京都大学基礎物理学研究所 集中講義 「近傍宇宙論(銀河考古学)で探るダークマターの正体」”