擬ニュートンポテンシャル (pseudo-Newtonian potential)

別名、Paczynski-Wiitaポテンシャルとも呼ばれるこのポテンシャルは、一般相対論から導出されるブラックホールの作る重力ポテンシャルの良い近似となるものです。具体的には以下のように書かれます。

\[\Phi_\mathrm{PN}(r) = - \frac{GM}{r-r_g} \tag{1}\]

ここで\(r\)はブラックホールからの距離、そして\(r_g = 2 GM / c^2\)はシュバルツシルト半径です。これを求めてみましょう。

導出

アインシュタイン方程式の係数\(\kappa = 8\pi G/c^4\)を求めるときに用いた、弱重力場極限でのメトリック

\[(g_{\mu \nu}) = \left( \begin{array}{cccc} -(1+h_{00}) & & & \mathbf{0} \\ & 1+h & & \\ & & 1+h & \\ \mathbf{0} & & & 1+h \end{array} \right) \tag{2}\]

を用います。このとき、一般相対論の弱重力場極限がニュートン力学を再現するという制約から

\[h_{00} = \frac{2 \Phi_\mathrm{GR}}{c^2} \tag{3}\]

のように求まるのでした。さらに球対称重力場の時空計量を

\[(g_{\mu \nu}) = \left( \begin{array}{cccc} -e^{2\Phi} & & & \mathbf{0} \\ & e^{2\Lambda} & & \\ & & r^2 & \\ \mathbf{0} & & & r^2 \sin^2 \theta \end{array} \right) \tag{4}\]

と仮定してシュバルツシルト時空の計量を求めると

\[\Phi (r) = \frac{1}{2} \ln (1-r_g / r) \tag{5}\]

と求まります。
(2), (4)式での00成分を比較すると

\[- 1 - \underbrace{h_{00}}_{(3)} = - \left( 1+ \frac{2 \Phi_\mathrm{GR}}{c^2}\right) \underbrace{\simeq}_{\Phi_\mathrm{GR}/c^2 \ll 1} - e^{2\Phi_\mathrm{GR}/c^2} = - e^{2\Phi}\]

ここで、今考えているのはブラックホールの近傍ではなく\(r \gg r_g\)のような十分遠方であり、\(\Phi_\mathrm{GR} / c^2 \ll 1\)の場合を考えました。\(e\)の肩の比較と(5)式より

\[\Phi_\mathrm{GR} = \frac{c^2}{2} \ln (1-r_g/ r) = - \frac{c^2}{2} \ln \frac{r}{r-r_g} = - \frac{c^2}{2} \ln \left( 1 + \frac{r_g}{r - r_g}\right) \tag{6}\]

となります。ここで\(r_g \ll r-r_g\)のようにシュバルツシルト半径よりも十分遠方の領域を考え、対数部分をテイラー展開を考えます。それを擬ニュートンポテンシャルと定義すると

\[\Phi_\mathrm{GR} \simeq - \frac{c^2}{2} \frac{r_g}{r-r_g} = - \frac{GM}{r-r_g} \equiv \Phi_\mathrm{PN}\]

のように、(1)式が求まります。

ニュートン、擬ニュートン、一般相対論の比較

それぞれのポテンシャルをまとめると以下のようになります。

\[\Phi_\mathrm{N} = - \frac{GM}{r}, \quad \Phi_\mathrm{PN} = - \frac{GM}{r-r_g} , \quad \Phi_\mathrm{GR} = \frac{c^2}{2} \ln (1-r_g/r) \tag{7}\]

これを描画すると、以下のようになります。ここで、この描画のための\(r_g = 2GM/c^2 = 1, GM=1, c^2 = 2\)のように規格化して計算を行いました。

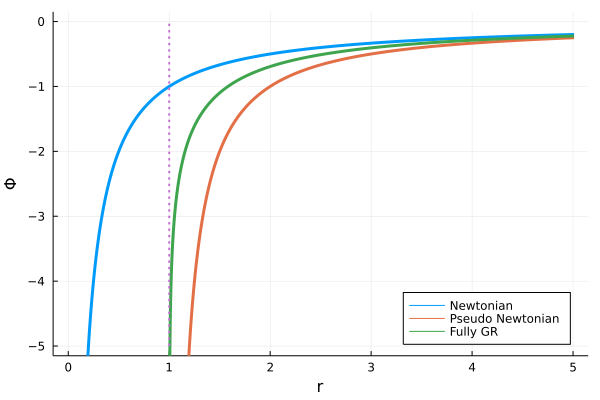
上図の点線はシュバルツシルト半径の位置を表します。ニュートンポテンシャルでは\(r<r_g\)の領域でも有限の値を持ちます。しかし一般相対論からしっかり考えた\(\Phi_\mathrm{GR}\)および、その近似である\(\Phi_\mathrm{PN}\)では\(r = r_g\)でマイナス無限大に発散しています。
続いて、この中心力ポテンシャル中において角運動量を持つ質点が運動する場合の有効ポテンシャルを見てみましょう。古典力学においては重力ポテンシャルに遠心力\(\ell^2 / 2 r^2\)を加えて

\[\Psi_\mathrm{N} = - \frac{GM}{r} + \frac{\ell^2}{2 r^2} \tag{8}\]

となります。ここで角運動量を\(\ell\)と置きました。続いて擬ニュートンポテンシャル中での運動における有効ポテンシャルです。(8)式からの類推より

\[\Psi_\mathrm{PN} = - \frac{GM}{r-r_g} + \frac{\ell^2}{2 r^2} \tag{9}\]

となります。一般相対論での有効ポテンシャルはISCOを求めたときの途中式より

\[\Psi_\mathrm{GR} = \frac{c^2}{2} \left( 1- \frac{r_g}{r} \right) \left( 1 + \frac{\ell^2}{c^2 r^2}\right) \tag{10}\]

です。これを描画したものが下図です。ここでも描画のために\(r_g = 2 GM/c^2 = 1, GM=1, c^2 = 2\)のように規格化して計算を行いました。

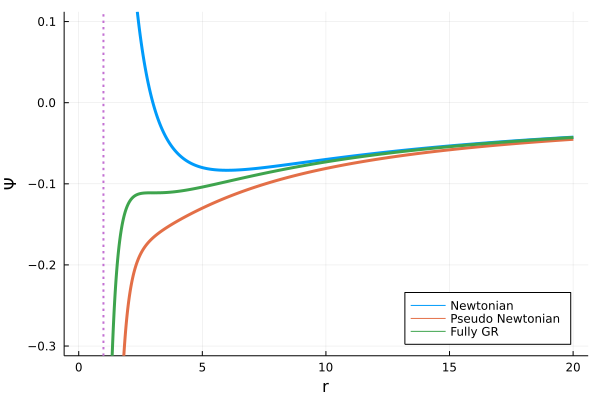
またこのグラフでは角運動量を\(\ell = \sqrt{3} r_g c (= \sqrt{6})\)としています(このとき\(\Psi_\mathrm{GR}\)では、\(r=3r_g\)にISCOが出現します)。さらに縦軸を合わせるために、一般相対論に関しては\(\Psi_\mathrm{GR}-1\)を描画しています。このグラフからわかるように、擬ニュートンポテンシャルはISCOを再現できていません。しかし遠心力バリアが存在するニュートン有効ポテンシャルとは異なり、\(r=r_g\)付近でブラックホールに(角運動量に関係なく)落ちていく様子が再現されています。

参考文献

[1] 福江純, “らくらく相対論入門その1: 擬ニュートンポテンシャルの特徴”
[2] Abramowicz, 2009, “The Paczyński-Wiita potential -A step by step derivation”
[3] Paczyński & Wiita, 1980, “Thick Accretion Disks and Supercritical Luminosities”
[4] 高橋博之, “ブラックホール降着円盤入門”