Table of contents
3.3.2 水素原子
自由状態は虚数の量子数\(n=ik\)を持つとみなします。(3.27)式にこれを代入すると、Bound-free遷移に対するOscillator strengthは
\[f_{n'k} = \frac{32}{3\pi \sqrt{3}} \left( \frac{1}{n'^2} + \frac{1}{k^2} \right)^{-3} \frac{1}{n'^5 k^3} g_{II} (n', k) \tag{3.39}\]と書くことができます。ここで\(g_{II}(n', k)\)はBound-free Gaunt factorです。
この過程で吸収される光の振動数は
です。ここで\({\mathcal R}= \frac{2\pi^2 \mu_{\rm H} e^4}{h^2}\)はRydberg定数を表します。水素原子1個あたりのBound-freeの吸収係数は
\[\alpha_\nu d\nu = \frac{\pi e^2}{mc} f_{n' k} \frac{dk}{d\nu}d\nu\](3.40)式より
\[h d\nu = - \frac{2{\mathcal R}}{k^3} dk \ \Longrightarrow \ \frac{dk}{d\nu} = -\frac{hk^3}{2 {\mathcal R}}\]を用いて
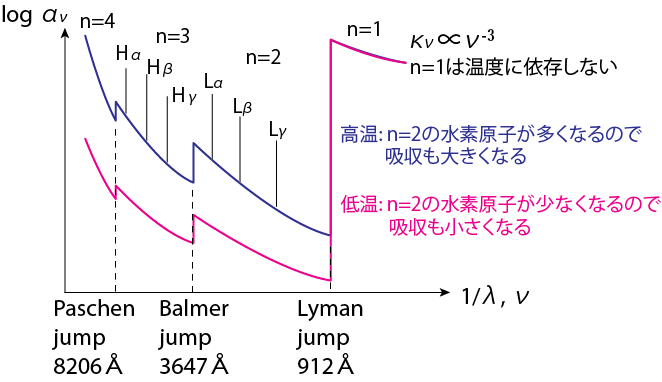
\[\alpha_\nu = \frac{\pi e^2}{mc} \left( \frac{16}{3\pi \sqrt{3}} \right) \frac{\mathcal R^2}{n'^5 h^2 \nu^3}g_{II} (n', \nu) \tag{3.41}\]を得ます。Bound-free吸収係数は\(\nu_n > \frac{\mathcal R}{hn^2}\)で値を持ち、近似的に\(\nu^{-3}\)に比例します。
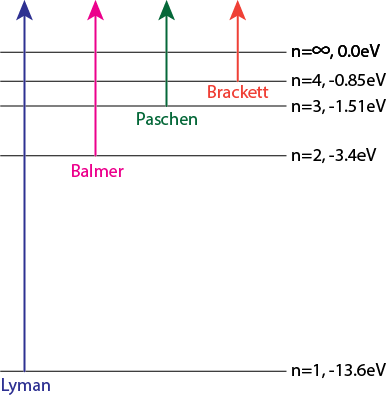
以下は中性水素の吸収端です。
| n | 波長(Å) | 名前 | 領域 |
|---|---|---|---|
| 1 | 912 | Lyman | 紫外 |
| 2 | 3647 | Balmer | 紫外と青の中間 |
| 3 | 8206 | Paschen | 赤外 |
| 4 | 14588 | Brackett | 赤外 |
| 5 | 22790 | Pfund | 赤外 |
3.3.3 Negative Hydrogen Ion
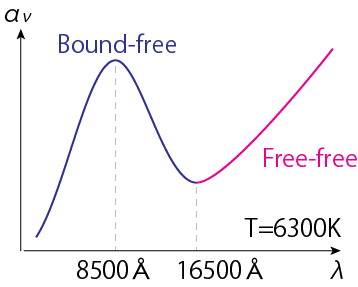
水素原子の電子の存在は偏っているため、もう1つ電子がくっついて負の電荷を持つNegative hydrogen ion \({\rm H}^{-1}\)が存在できます。必要な電子は、その他の重元素から供給されます。その結合エネルギーは0.754eVと小さいため、高温の状態では存在できません。しかし、太陽やそれよりも温度が低い恒星の大気では吸収係数に重要な貢献をします。実際、太陽大気ではNegative hydrogen ionが吸収の大きな割合を占めます。Negative hydrogen ionはBound-free, Free-free過程で光の吸収と発光を行います。Bound-free吸収は16500Å (1.65\(\mu\)m)より短い波長の光で起こり、吸収の最大は8500Åです。\({\rm H}^{-1}\)イオンのFree-free吸収は赤外域で大きいという特徴があります。