Table of contents
ラバール管 (Laval nozzle)
ラバール管流の解の振る舞い
断面が変化する管の中を流れる定常な圧縮性流体は、圧縮性流体の特徴が亜音速流\((v<C_s)\)と超音速流\((v>C_s)\)でどのように異なるかを示す、面白い例です。 さらにその流れの特徴は、球対称な点源重力場中の定常流にも、ほとんど同じように現れます。
次の図に示すように、管の断面積\(A\)が十分ゆっくりと滑らかに現象し、最小値\(A_c\)を過ぎると徐々に増大する管 (ラバール管)の中を流れる流体の運動を考えましょう。 ただし、ここで考える流れは断熱的であるとします。
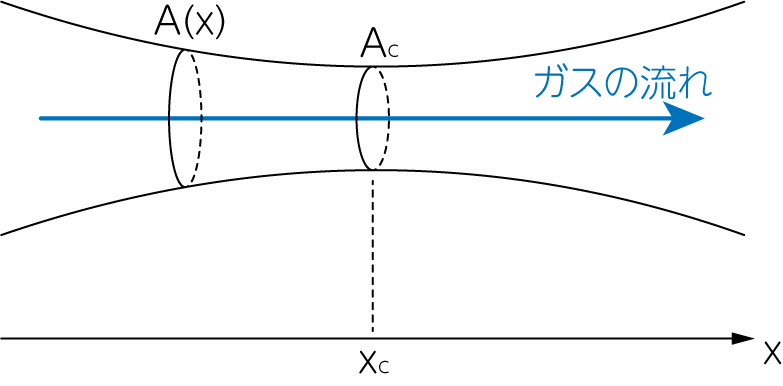
ラバール管の概略図。
定常流を考えているため、連続の式は
\[\nabla \cdot (\rho \mathbf{v}) = 0 \ \Longrightarrow \ \rho v A = (一定) \tag{1}\]となります。 管に沿って座標\(x\)をとることにすると、運動方程式は
\[v \frac{dv}{dx} = - \frac{1}{\rho} \frac{dP}{dx} \underbrace{=}_{P = K\rho^\gamma} - \frac{1}{\rho} K \gamma \rho^{\gamma -1} \frac{d\rho}{dx} = - \frac{\gamma P}{\rho^2} \frac{d\rho}{dx} \underbrace{=}_{C_s^2 = \frac{\gamma P}{\rho}} - \frac{C_s^2}{\rho} \frac{d\rho}{dx} \tag{2}\]のように与えられます。 (1)式の両辺の対数を取り、その微小量が満たす式から、微分方程式を得てみましょう。
\[\begin{align} \ln (\rho v A) = \ln \rho + \ln v + \ln A = (一定) & \Longrightarrow \ \frac{d\rho}{\rho} + \frac{dv}{v} + \frac{dA}{A} = 0 \notag \\ & \Longrightarrow \ \frac{1}{\rho} \frac{d\rho}{dx} = - \frac{1}{v} \frac{dv}{dx} - \frac{1}{A} \frac{dA}{dx} \tag{3} \end{align}\]この式を(3)式に代入すると
\[v \frac{dv}{dx} = \frac{C_s^2}{v} \frac{dv}{dx} + \frac{C_s^2}{A} \frac{dA}{dx} \ \Longrightarrow \ (M^2 - 1) \frac{1}{v} \frac{dv}{dx} = \frac{1}{A} \frac{dA}{dx} \tag{4}\]のようになります。 ここで\(M = \frac{v}{C_s}\)は、マッハ数を表します。
(4)式から、流体の運動が亜音速(\(M<1\))では、\(\frac{dA}{dx}<0\)(だんだん管が細くなる)なら加速し、\(\frac{dA}{dx}>0\)(だんだん管が太くなる)なら減速することがわかります。 これは、たとえばホースで花壇に水やりをする場合などでみられるように、ホースの先を指で押さえて水の出口を細く絞ることで、水が勢いよく噴出する様子を表しています。 一方、超音速(\(M>1\))の場合は、\(\frac{dA}{dx}<0\)なら減速、\(\frac{dA}{dx}>0\)なら加速することがわかります。 以上の説明から、\(\frac{dA}{dx}<0\)で\(M<1\)であり、\(\frac{dA}{dx} = 0\)(管の面積が最小となる位置)で\(M=1\)に達し、その後\(\frac{dA}{dx}>0\)の領域で\(M>1\)となるような流れでは、流れの至るところで\(\frac{dv}{dx}\)が正となり、加速されつづける流れであることがわかります。 これを遷音速解と呼びます。 そして流れにおいて\(A(x)\)が最小となる場所\(x = x_c\)で\(M=1\)となる点を、臨界点(critical point)と呼びます。 (4)式をさらに整理しましょう。 そのために、以下のような計算を行います。
(5), (6)式より
\[\frac{dM}{dx} = \frac{1}{C_s} \frac{dv}{dx} + \frac{v}{C_s^2} \frac{\gamma -1}{2C_s} v \frac{dv}{dx} = \frac{M}{v} \frac{dv}{dx} \left( 1 + \frac{\gamma-1}{2} M^2\right) \tag{7}\](4)式より
\[\frac{dM}{dx} = \frac{M}{M^2 - 1} \frac{1}{A} \frac{dA}{dx} \left( 1 + \frac{\gamma-1}{2} M^2\right) \tag{8}\]を得ます。
臨界点での勾配
臨界点\(x=x_c\)においては\(M^2 - 1 = 0, \frac{dA}{dx} = 0\)となるため、(8)式から直接\(\frac{dM}{dx}\)を求めようとすると、\(0/0\)の不定形となります。 そこで、臨界点での振る舞いを調べるために、管の断面積が最小となる位置\(x = x_c\)の周りでテイラー展開を行いましょう。
\[A \approx A_0 + \underbrace{\left. \frac{dA}{dx} \right\vert_{x_c}}_{=0} \delta x + \frac{1}{2} \left. \frac{d^2A}{dx^2} \right\vert_{x_c} \delta x^2 \equiv A_0 + A_2 \delta x^2 \tag{9}\] \[M = 1 + \left. \frac{dM}{dx} \right\vert_{x_c} \delta x \equiv 1 + M_1 \delta x \tag{10}\]これらを(8)式に代入すると
\[\begin{aligned} \left. \frac{dM}{dx} \right\vert_{x_c} &= M_1 = \frac{1 + M_1 \delta x}{2M_1 \delta x + M_1^2 \delta x^2} \frac{1}{A_0 + A_2 \delta x^2} 2 A_2 \delta x \left\{ 1 + \frac{\gamma-1}{2} (1 + 2 M_1 \delta x + M_1^2 \delta x^2) \right\} \notag \\ &= \frac{1 + M_1 \delta x}{2M_1 + M_1^2 \delta x} \frac{2 A_2 }{A_0 + A_2 \delta x^2} \left\{ 1 + \frac{\gamma-1}{2} (1 + 2 M_1 \delta x + M_1^2 \delta x^2) \right\} \notag \\ &\xrightarrow{\delta x \rightarrow 0} \frac{1}{M_1} \frac{A_2}{A_0} \frac{\gamma + 1}{2} \end{aligned}\]となるため、最終的に
\[M_1 = \left. \frac{dM}{dx} \right\vert_{x_c} = \pm \sqrt{\frac{\gamma+1}{2} \frac{A_2}{A_0}} \tag{11}\]を得ます。 プラス符号は、\(x<x_c\)から亜音速で出発して、臨界点を通り、\(x>x_c\)で超音速となる解に対する勾配を表してます。 マイナス符号は、\(x<x_c\)で超音速だった流れが減速を受けて、臨界点を通り、\(x>x_c\)で亜音速となる解に対応しています。 (8)式において\(M \rightarrow -M\)のようにしても方程式が不変であることからも分かるように、亜音速から超音速に繋がる解が存在すれば、同様に超音速から亜音速に繋がる解も存在することがわかります。
よどみ点からの加速限界
このラバール管の断面積を無限に広げれば、無限に加速できるように思われるかもしれません。 しかし次に示すように、当然そのようにはなりません。 (8)式で\(A \rightarrow \infty\)のようにすると、右辺がゼロとなることから、\(\frac{dM}{dx}\)もゼロとなり、流れの速度は有限値で頭打ちとなることがわかります。 この限界速度を求めてみましょう。 ここでは、流体は初速ゼロから出発し、臨界点を通って超音速まで加速されたとします。 (4)式の両辺を\(x=x_c\)から超音速領域の適当は座標\(x=x_1\)まで積分しましょう。
\[(左辺) = \int_{x_c}^{x_1} \frac{M^2 - 1}{v} \frac{dv}{dx} dx = \int_{v_c}^{v_1} \frac{M^2 - 1}{v} dv \tag{12}\] \[(右辺) = \int_{x_c}^{x_1} \frac{1}{A} \frac{dA}{dx} dx = \int_{A_c}^{A_1} \frac{1}{A} dA = \log \frac{A_1}{A_c} \tag{13}\]ベルヌーイの定理より、流体の速度がゼロとなる場所(よどみ点)での位置の物理量に添字0をつけて表すと
\[\frac{1}{2} v^2 + \frac{C_s^2}{\gamma-1} = \frac{C_{s, 0}^2}{\gamma -1} \ \Longrightarrow \ C_s^2 = C_{s, 0}^2 - \frac{\gamma-1}{2} v^2 \tag{14}\]のようになります。 (12)式の積分をさらに進めるために、被積分関数を速度\(v\)で表しましょう。
\[M^2 = \frac{v^2}{C_s^2} = \frac{v^2}{C_{s, 0}^2 - \frac{\gamma-1}{2} v^2} \notag\] \[\frac{M^2 - 1}{v} = \frac{v^2 - \left( C_{s, 0}^2 - \frac{\gamma-1}{2} v^2 \right)}{ v \left( C_{s, 0}^2 - \frac{\gamma-1}{2} v^2 \right)} = \frac{\frac{\gamma+1}{2} v^2 - C_{s, 0}^2}{ v \left( C_{s, 0}^2 - \frac{\gamma-1}{2} v^2 \right)} \underbrace{=}_{部分分数分解} - \frac{1}{v} + \frac{v}{C_{s, 0}^2 - \frac{\gamma-1}{2} v^2} \tag{15}\](15)式を(12)式に代入し、積分を実行すれば
\[\left[ - \ln v - \frac{1}{\gamma-1} \ln \left( -\frac{\gamma-1}{2}v^2 + C_{s, 0}^2\right) \right]_{v_c}^{v_1} = \log \frac{A_1}{A_c} \tag{16}\]\(A_1 \rightarrow \infty\)のとき、右辺は発散します。 ここから同様に左辺が発散するには、対数の中身である\((\cdots ) = 0\)となれば良いでしょう。 よって、よどみ点からの加速限界が
\[v_1 = \sqrt{\frac{2}{\gamma-1}} C_{s, 0} \tag{17}\]と求まります。 これはベルヌーイの定理(14)式において、\(v_1 \gg C_{s, 1}\)まで加速されたとして
\[\frac{1}{2} v_1^2 = \frac{C_{s, 0}^2}{\gamma-1} \tag{18}\]のようにして求めたものと一致します。 ここから、ラバール管による加速限界が、ベルヌーイの定理と矛盾しないこともわかりました。
ラバール管を用いた実験の設計
入り口での圧力\(P_\infty\)を固定したとき、実際にどのような解の状態がラバール管で実現されるかは、出口での圧力\(P_e\)(背圧, back pressure)に依存します。 下図は、入り口で亜音速であるとして、その概略を示したものです。
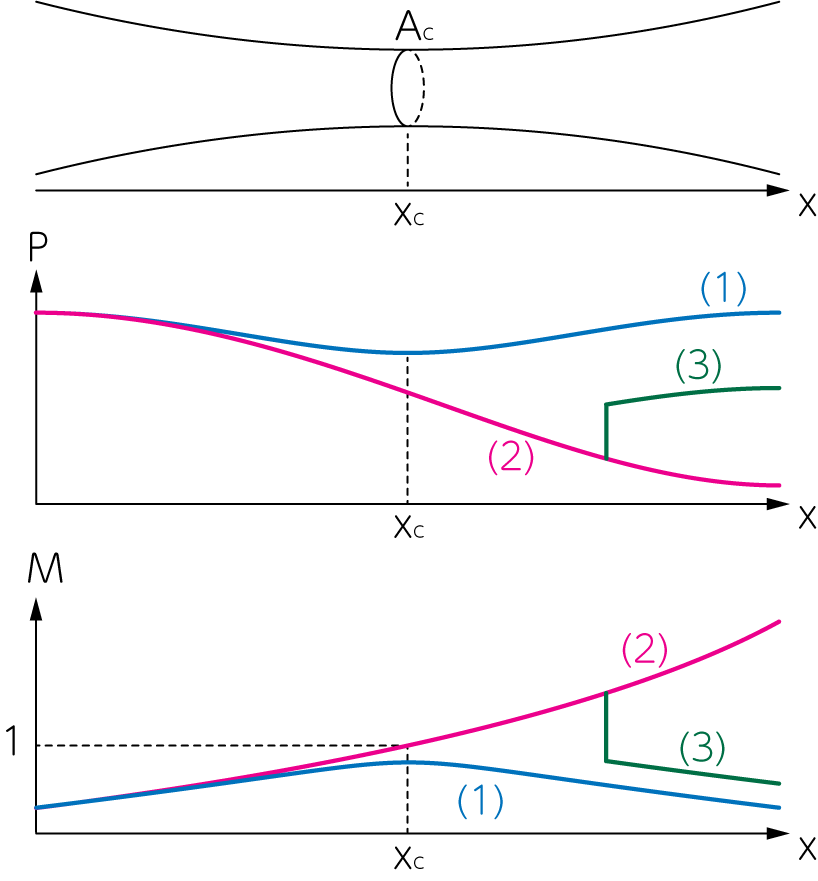
ラバール管での流れの様子を示したもの。(1)は常に亜音速の流れ、(2)は遷音速流、(3)は臨界点を通るが衝撃波を経験することで最終的に亜音速となる流れ。
圧力が高い場合、流れは臨界点を通過することなく、常に亜音速のままラバール管から出てしまいます。 音速点を通るように背圧を下げてやると、流れは超音速まで加速されます。 しかし背圧が中途半端に高い場合、せっかく音速点を通って超音速となっても、その超音速流は出口のガスと接続するために衝撃波を起こして亜音速流となります。 衝撃波の下流側の解は、衝撃波のランキン・ユゴニオ条件を満たすものが選ばれます。 どのような流れを実現したいかで、ラバール管出口の背圧や、ラバール管の断面積を詳細に設定する必要があるでしょう。
参考文献
[1] 北島歓大, 2025, “相対論的流体力学の粒子法的数値計算法の開発及び高速噴流の解析”
[2] 田中秀和, “宇宙流体力学”
[3] 坂下志郎, 池内了, “宇宙流体力学”
[4] 福江純, 和田桂一, 梅村雅之, “宇宙流体力学の基礎”