ISCO
最も内側の安定円軌道(Innter-most Stable Circular Orbit)のことです。これより内側のブラックホール側には安定円軌道が存在しないため、ブラックホール周囲の降着円盤も内側で穴の空いたドーナツのような構造となります。
以下ではシュバルツシルト時空におけるISCOを求めてみましょう。
シュバルツシルト計量
シュバルツシルト計量は以下のように与えられます。
\[ds^2 = -(1-\frac{2GM}{c^2 r}) c^2 dt^2 + (1-\frac{2GM}{c^2 r})^{-1} dr^2 + r^2 d\theta^2 + r^2 \sin^2 \theta d \varphi^2\]シュバルツシルト半径を\(r_g = 2GM/c^2\)と定義すると
\[g_{tt} = -(1-\frac{r_g}{r}), \ g_{rr} = \frac{1}{1-\frac{r_g}{r}}, \ g_{\theta \theta} = r^2, \ g_{\varphi \varphi} = r^2 \sin^2 \theta\]粒子の測地線方程式
粒子の測地線方程式より
\[m \frac{dp_\nu}{d\tau} = \frac{1}{2} g_{\beta \mu, \nu} p^\mu p^\beta\]\(g_{\beta \mu}\)の依存性から\(g_{\beta \mu , t} = 0, g_{\beta \mu, \varphi} = 0\)がわかるので
\[p_t = {\rm Const} = mE, \ p_\varphi = {\rm Const} = m \ell\]ここで\(E, \ell\)は単位質量あたりのエネルギーと角運動量を意味することが、この後の変形でわかります。
式変形
球対称の仮定より角運動量が保存し、粒子の運動は一平面に限定できます。簡単のため、\(\theta=\pi/2\)の平面上での運動を考え、\(d\theta=0\)としましょう。
\[p^\alpha p_\alpha = m^2 u^\alpha u_\alpha = m^2 \gamma^2 (-c^2 + v^2) = -m^2 c^2\]と
\[p^0 = g^{0\beta} p_\beta = g^{00} p_0 = -\frac{1}{1-\frac{r_g}{r}} mE\] \[p^\varphi = g^{\varphi \beta} p_\beta = g^{\varphi \varphi} p_\varphi = \frac{m\ell}{r^2 \sin^2\theta}\]より
\[-m^2 c^2 = g_{\alpha\beta} p^\alpha p^\beta = - (1-\frac{r_g}{r} ) \frac{1}{(1-\frac{r_g}{r})^2} m^2 E^2 + m^2 \frac{1}{1-\frac{r_g}{r}} \left( \frac{dr}{d\tau} \right)^2 + r^2 \left( \frac{m\ell}{r^2} \right)^2\]途中、\(p^r = m dr/d\tau, p^\theta = 0, \sin \theta = 1\)と置きました。これ式変形すると
\[\left(\frac{dr}{d\tau} \right)^2 = E^2 - (1-\frac{r_g}{r}) (c^2 + \frac{\ell^2}{r^2})\]有効ポテンシャル
有効ポテンシャルを
\[\Psi_{\rm eff} = (1-\frac{r_g}{r}) (c^2 + \frac{\ell^2}{r^2})\]で定義するとき、運動は\(E^2 > \Psi_{\rm eff}\)を満たす領域でのみ可能です。
ISCO
円軌道にある粒子は
\[\frac{dr}{d\tau} = 0, \ \frac{d\Psi_{\rm eff}}{dr} = 0\]の2つを満たさなければなりません。またこの軌道の安定性は\(\frac{d^2 \Psi_{\rm eff}}{dr^2}\)の正負で決められます。\(\frac{d^2 \Psi_{\rm eff}}{dr^2} > 0\)(下に凸)なら安定となることがわかります。
ここでは\(\frac{d\Psi_{\rm eff}}{dr} = 0\)からその半径を求めてみましょう。
2次方程式の解の公式より
\[r = \frac{\ell^2 \pm \ell^2 \sqrt{1-3r_g^2 c^2 / \ell^2}}{r_g c^2}\]\(\ell < \sqrt{3} r_g c\)のとき虚数解となり、\(\ell\)に対応する円軌道が存在しないことがわかります。よって臨界値となるのは
\[\ell_c = \sqrt{3} r_g c\]そしてこのときの円軌道半径は
\[r_c = 3 r_g \equiv r_{\rm ISCO}\]が最も内側の安定円軌道の半径となることがわかります。
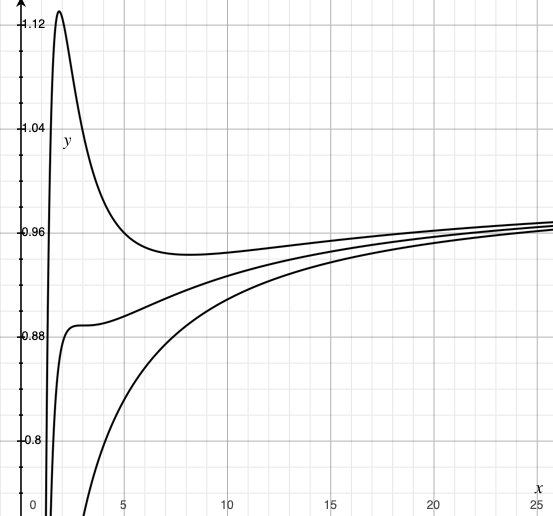
物理的解釈
粒子の角運動量が\(\ell_c\)よりも小さい場合は、一般相対論的な効果により安定な円軌道は存在せず、遠心力も重力に逆らうだけの大きさも持てずに粒子は中心に落下します。これは以下のように考えることができます。
- 球対称時空なので、角運動量は保存している
- 角運動量が保存したまま動径方向内側に移動すると、角速度が大きくなる
- 角速度が大きくなるということは、テスト粒子の速度も大きくなる。すなわち運動エネルギーも増加する
- 相対論ではエネルギーと質量は等価なので、運動エネルギーの増加は質量の増加を意味する。
このような論理展開から、内側に行くほどテスト粒子の質量は大きくなり、結果としてテスト粒子の感じる重力の大きさは遠心力以上になります。このような理由から、ニュートン力学では遠心力バリアに阻まれて到達できなかった、ブラックホールの存在する\(r=0\)へと吸い込まれていきます。
実際に一般相対論的な有効ポテンシャルを式変形してみましょう。
最後の\(c^2/2\)は定数なので、ポテンシャルの概形を変化させません。よってここでは最初の3つの項について考察します。第一項は古典力学における万有引力ポテンシャルです。そこに遠心力ポテンシャルが加わっていることは同じなのですが、その遠心力ポテンシャルに\(- r_g / r\)の補正が入っています。先程の説明にある通り、(運動エネルギー) \simeq (質量エネルギー\(m c^2\))の効果により、重たくなることで遠心力が弱まることを表しています。
降着円盤の物理
降着円盤の場合、ガス円盤はその粘性や磁場によって角運動量が減少しながら落ちていきます。それによって角運動量が\(r_{\rm ISCO}\)付近で\(\ell_c\)以下になれば、それ以上角運動量を抜き取る機構がなくても、一般相対論的な効果によってブラックホールに落ちてゆくことができます。