重力レンズ
ここでは弱い重力場の極限での光の測地線方程式の空間成分から、重力レンズ効果を導出してみましょう。
簡単な導出
メトリックテンソルが弱重力場極限
\[(g^{\mu \nu}) = \left( \begin{array}{cccc} -(1-2\Phi / c^2) & & & {\bf 0}\\ & 1+2\Phi/c^2 & & \\ & & 1+2\Phi/c^2 & \\ {\bf 0} & & & 1+2\Phi/c^2 \end{array} \right)\]で書けるものとします。次に4元共変波数ベクトルを\((k_0, k_1, 0, 0)\)のようにして、光の進行方向を\(x^1\)方向にとります。
\[k^0 = \frac{\partial \bar{x}^0}{\partial x^0}\bar{k}^0 = -(1+ \frac{\Phi}{c^2}) \frac{\omega}{c}\] \[k^1 = \frac{\partial \bar{x}^1}{\partial x^1}\bar{k}^1 = (1- \frac{\Phi}{c^2}) k\]ここで\(k^0 = \eta_{00} k^0 = -\omega /c\)です。時刻\(t\)に位置\(x\)にあった波面が微小時間\(dt\)後に\(x+dx\)に移動したとしましょう。位相一定面\(k^\mu x_\mu = {\rm Const.}\)の方程式は
\[k_0 ct + k_1 x = k_0 c(t+dt) + k_1(x+dx)\]となります。この式から同位相面が伝搬する速度すなわち位相速度が微小量の一次までの式を構築すると以下のように計算できます。
\[v_p = \frac{dx}{dt} = -c\frac{k_0}{k_1} =(1+\frac{2\Phi}{c^2}) \frac{\omega}{k}\]最後の式の右辺の\(\omega/k\)は局所慣性系での光の位相速度\(c\)です。よってこの式は、重力場の存在は屈折率
\[n = 1-\frac{2\Phi}{c^2} > 1\]の媒質と同じ役割を果たすことを意味します。
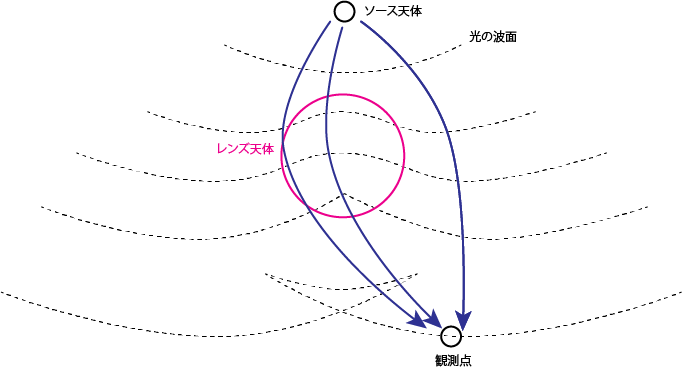
厳密な導出
メトリックテンソルは上述と同じもので与えられ、\(\Phi\)は時間に陽に依存しないとします。光の4元運動量の空間成分は
\[p^i = \frac{dx^i}{d\lambda} = \frac{dx^0}{d\lambda} \frac{dx^i}{dx^0} = p^0 \gamma^i\]ここで\(\gamma^i = dx^i / dx^0\)で定義される3次元ベクトル\(\boldsymbol{\gamma}\)は光の進行方向を表すベクトルです。重力場が存在しない時の進行方向ベクトルを\(\bar{\gamma}^i\)とし、重力場の存在によって変更を受けた光の進行方向を\(\delta \gamma^i\)と表現します。\(\delta \gamma^i\)は\(|\Phi/c^2|\)と同じオーダーの微小量です。
測地線方程式の空間成分より
途中の式は、慣性系では
\[0 = \eta_{\mu \nu} \bar{p}^\mu \bar{p}^\nu = \eta_{\mu \nu} \frac{d\bar{x}^\mu}{d\lambda} \frac{d\bar{x}^\nu}{d\lambda} = -\left( \frac{d\bar{x}^0}{d\lambda}\right)^2 + \delta_{ij} \frac{d\bar{x}^0}{d\lambda} \frac{d\bar{x}^i}{d \bar{x}^0} \frac{d\bar{x}^0}{d\lambda} \frac{d\bar{x}^j}{d\bar{x}^0} = \left( \frac{d\bar{x}^0}{d\lambda} \right)^2 (-1 + \delta_{ij} \bar{\gamma}^i \bar{\gamma}^j)\]となることから証明されます。
ここで
\[p^0 = (1-\frac{\Phi}{c^2}) \frac{h\nu}{c}\] \[p_i = g_{ij} p^j = (1-\frac{3 \Phi}{c^2}) \frac{h\nu}{c} (\bar{\gamma}^i + \delta \gamma^i) = ((1+ \frac{\Phi}{c^2}) \frac{h\nu}{c}-\frac{4}{c^2} \Phi \frac{h\nu}{c} ) (\bar{\gamma}^i + \delta \gamma^i)\]です。以上をまとめると
\[\frac{1}{c} \frac{dp_i}{dt} = -\frac{4}{c^2} \bar{\gamma}^i \frac{h\nu}{c} \frac{d\Phi}{dt} + \frac{h\nu}{c} \frac{d \delta \gamma^i}{dt}\]ここで
\[\frac{d \bar{\gamma}^i}{dt} = 0\]すなわち0次の光の進行方向は時間変化しないこと、そして光子のエネルギー変化は微小量の1次であることから
\[\frac{d}{dt} ((\Phi)h\nu) = h\nu \frac{d\Phi}{dt}, \ \frac{d}{dt} ((\Phi)h\nu) = h\nu \frac{d\Phi}{dt}\]と近似できること、さらに重力赤方偏移の式から
\[h\nu (1+\frac{1}{c^2} \frac{\Phi}{dt}) = \frac{2h\nu}{c^2} \frac{\partial \Phi}{\partial t} \underbrace{=}_{時間に陽に依存しない} \frac{2h\nu}{c^2} \frac{d \Phi}{d t}\]より
\[\frac{1}{c} \frac{dp_i}{dt} = -\frac{4}{c^2} \bar{\gamma}^i \frac{h\nu}{c} \frac{d\Phi}{dt} + \frac{h\nu}{c} \frac{d \delta \gamma^i}{dt} = -\frac{4}{c^2} \bar{\gamma}^i \bar{\gamma}^k \frac{h\nu}{c} \Phi_{, k} + \frac{h\nu}{c} \frac{d \delta \gamma^i}{dt} \tag{2}\](1), (2)式を比較して
\[\frac{1}{c} \frac{d \delta \gamma^i}{dt} = -\frac{2}{c^2} \Phi_{, i} + 4 \frac{\bar{\gamma}^k}{c} \Phi_{, k} \bar{\gamma}^i \tag{3}\]を得ます。
屈折角の方程式
重力場中の光の進行方向を決定する上の方程式をさらに整理して、重力レンズ効果による屈折角を決定する方程式を導出してみましょう。
\(\boldsymbol{\gamma}\)に直交する単位ベクトルを\(\boldsymbol{\gamma}_{\perp, 1}\)、さらにこの両方に直交する単位ベクトルを\(\boldsymbol{\gamma}_{\perp, 2}\)とします。\(\delta \boldsymbol{\gamma}\)を0次の光の進路に平行な成分\(\delta \gamma_{\parallel}\)とそれに垂直な成分\(\delta \gamma_{\perp, 1}, \delta \gamma_{\perp, 2}\)として、以下のように分解します。
これらを用いて、重力場の存在による光の進行方向の変化を記述する方程式(3)に\(\bar{\gamma}^i, \bar{\gamma}^i_{\perp, 1}, \bar{\gamma}^i_{\perp, 2}\)をそれぞれかけて\(i\)で縮約をとり、(3)式を
\[\frac{1}{c} \frac{d \delta \gamma_\parallel}{dt} = -\frac{2}{c^2} \bar{\gamma}^i \Phi_{, i} + 4 \frac{\bar{\gamma}^k}{c} \Phi_{, k}\] \[\frac{1}{c} \frac{d \delta \boldsymbol{\gamma}_\perp}{dt} = -\frac{2}{c^2} \nabla_{\perp} \Phi \tag{4}\]ここで\(\delta \boldsymbol{\gamma}_\perp = \delta \gamma_{\perp, 1} \boldsymbol{\gamma}_{\perp, 1} + \delta \gamma_{\perp, 2} \boldsymbol{\gamma}_{\perp, 2}\)です。また\(\nabla_\perp\)は光の0次の経路に垂直な方向への勾配を表しています。
(4)式が光の進行方向がどのように曲がるかを記述する方程式です。これを0次の光の経路に沿って積分することにより
これらの結果は、光が伝搬する途中に存在する天体の重力によって、進行方向と垂直な方向に力を受けて光の進行方向が曲がることを示しています。これを重力レンズ効果と呼びます。\(\alpha = |\boldsymbol{\gamma}_\perp |\)は光の進行方向が正味曲がった角度を表しており、これを曲がり角(deflection angle)と呼びます。
重力レンズの式は光の波長に依存しないため、重力レンズ効果による天体の見え方も波長に依存しないことがわかります。
多くの天体の重力レンズ効果により曲がり角は非常に小さく、大きくても\(10^{-4}\)ラジアン程度です。したがって重力レンズによる曲がりが小さいとした上述の積分はよい近似になっていることがわかります。