Table of contents
ダランベール方程式の球面波解とその性質
ダランベール方程式
\[\Delta f(\mathbf{r}, t) - \frac{1}{c^2} \frac{\partial^2 f(\mathbf{r}, t)}{\partial t^2} = 0 \tag{1}\]の球面波について考察しましょう。球面極座標の動径座標を$R$とします。さらに以降では、関数$f$は動径座標と時刻のみの関数、すなわち\(f(R, t)\)とします。
球対称ダランベール方程式
3次元極座標のラプラシアンの導出については別記事やその他、ご自身にあったwebsiteを参照して下さい。これより
\[\nabla^2 = \frac{1}{R^2} \frac{\partial}{\partial R} \left( R^2 \frac{\partial}{\partial R}\right) + \frac{1}{R^2 \sin\theta} \frac{\partial}{\partial \theta} \left( \sin\theta \frac{\partial}{\partial \theta}\right) + \frac{1}{R^2 \sin^2\theta} \frac{\partial^2}{\partial \varphi^2}\]であることがわかります。今、関数は\(f(R, t)\)の形であることから
\[\frac{1}{R^2} \frac{\partial}{\partial R} \left( R^2 \frac{\partial f}{\partial R}\right) - \frac{1}{c^2} \frac{\partial^2 f}{\partial t^2} = 0 \tag{2}\]となります。
形式解の導出
解を\(f(R, t) = U(R, t) / R\)の形で求めます。よってこれを(2)式に代入しましょう。
\[\begin{align} &\frac{1}{R^2}\frac{\partial}{\partial R}\left( R^2 \frac{\partial }{\partial R} \left(\frac{U(R, t)}{R}\right)\right) - c^2\frac{\partial^2}{\partial t^2} \left( \frac{U(R, t)}{R}\right) = \frac{1}{R^2}\frac{\partial }{\partial R} \left( R^2 \frac{\frac{\partial U}{\partial R}R -U}{R^2}\right) - \frac{1}{c^2 R} \frac{\partial^2 U}{\partial t^2} \notag \\ &= \frac{1}{R^2} \left( \frac{\partial^2 U}{\partial R^2}+ \frac{\partial U }{\partial R} - \frac{\partial U}{\partial R}\right)-\frac{1}{c^2 R}\frac{\partial^2 U}{\partial t^2} = \frac{1}{R} \frac{\partial^2 U}{\partial R^2} -\frac{1}{c^2 R} \frac{\partial^2 U}{\partial t^2} = 0 \notag \\ &\Longrightarrow \ \frac{\partial^2 U}{\partial R^2} - \frac{1}{c^2} \frac{\partial^2 U}{\partial t^2} = 0 \tag{3} \end{align}\](3)式に\(\xi = R - ct, \eta = R + ct\)のような変数変換を施します。微分の連鎖律から
\[\frac{\partial }{\partial R} = \frac{\partial \xi}{\partial R}\frac{\partial }{\partial \xi} + \frac{\partial \eta}{\partial R} \frac{\partial}{\partial \eta} = \frac{\partial }{\partial \xi} + \frac{\partial }{\partial \eta}\] \[\frac{\partial }{\partial t} = \frac{\partial \xi}{\partial t}\frac{\partial }{\partial \xi} + \frac{\partial \eta}{\partial t} \frac{\partial}{\partial \eta} = -c\frac{\partial }{\partial \xi} + c\frac{\partial }{\partial \eta}\]より
\[\begin{align} &\frac{\partial^2 U(R, t) }{\partial R^2} -\frac{1}{c^2}\frac{\partial^2 U(R,t)}{\partial t^2} = \left( \frac{\partial }{\partial \xi}+ \frac{\partial}{\partial \eta}\right)^2 U(\xi, \eta) -\frac{1}{c^2} \left( -c \frac{\partial}{\partial \xi} + c \frac{\partial}{\partial \eta}\right)^2 U(\xi, \eta) \notag \\ &= \left( \frac{\partial^2}{\partial \xi^2} + 2\frac{\partial^2}{\partial \xi \partial \eta} + \frac{\partial^2}{\partial \eta^2} \right)U(\xi, \eta) - \left( \frac{\partial^2}{\partial \xi^2} - 2 \frac{\partial^2}{\partial \xi \partial \eta} + \frac{\partial^2}{\partial \eta^2}\right)U(\xi, \eta) \notag \\ &= 4\frac{\partial^2}{\partial \xi \partial \eta} U(\xi, \eta) = 0 \ \Longrightarrow \ \therefore \ \frac{\partial^2}{\partial \xi \partial \eta} U(\xi, \eta) = 0 \tag{4} \end{align}\](4)式より\(f(R, t) = g(\xi)/R, h(\eta)/R\)の2つがダランベール方程式の解になっていることを示しましょう。これらをダランベール方程式に代入して変形したものは、(4)式の\(U(\xi, \eta)\)を\(g(\xi), h(\eta)\)に置き換えたものに等しいです。
\[\frac{\partial^2}{\partial \xi \partial \eta} g(\xi) = \frac{\partial^2}{\partial \xi \partial \eta} g(\eta) = 0\]この式は恒等的に成り立つので、\(f(R, t) = g(\xi)/R, h(\eta)/R\)の2つはダランベール方程式の解であることがわかります。
形式解の物理的意味
得られた2つの解の物理的な考察をしてみましょう。
(i) \(f(R, t) = \frac{g(\xi)}{R} = \frac{g(R-ct)}{R}\)の性質
\(R=0\)から\(t=0\)に発信された情報(すなわち\(g(0)\))が\(R=r(>0)\)に到達する時刻が\(t=r/c\)になることを意味しています。またその情報の強度は\(1/r\)に減衰しています。
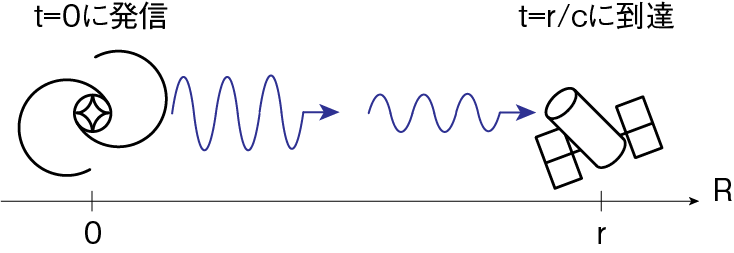
(ii) \(f(R, t) = \frac{h(\eta)}{R} = \frac{h(R+ct)}{R}\)の性質
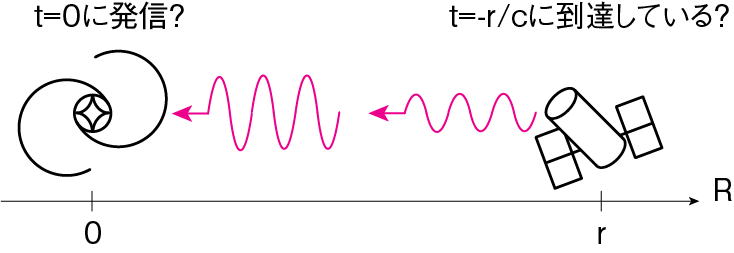
\(R=0\)から\(t=0\)に発信されるはずの情報(すなわち\(h(0)\))が\(R=r(>0)\)にはすでに\(t = -r/c\)の過去に存在していることになります。またその情報は\(R=0\)で\(t=0\)に発信されるはずの情報の\(1/r\)に減衰したものとなっています。これは情報が発信される前に存在することになるので、物理的には因果律に反する解を表現していることになります。
総括
(i), (ii)を総合すると
- \(f(R, t) = g(R-ct)/R\)はある時刻に原点で起こった事象の情報が、原点から外向きの球面波として伝搬する解(物理的に意味のある解)
- \(f(R, t) = h(R+ct)/R\)は原点である時刻に起こるはずの事象の情報が、事象が起こる前からはるか遠方より原点に向かって内向きの球面波として伝搬する解ということがわかります(物理的に意味のない解)。