Table of contents
スウィート・パーカーの磁気リコネクション (Sweet-Parker reconnection)
以下の図のように、反平行に並んでいる磁力線がinflowによって接近し、リコネクション(磁力線のつなぎ変え)が発生していると考えましょう。
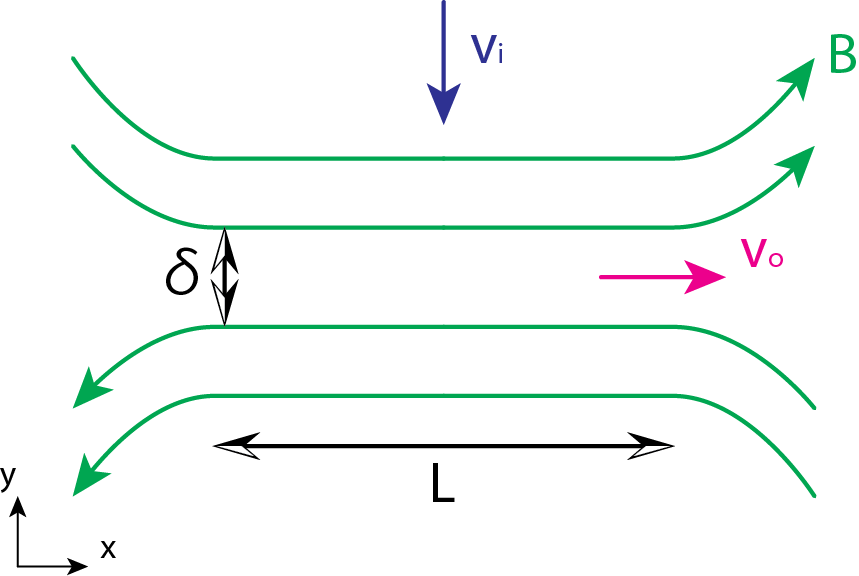
リコネクション率
簡単のため2次元非圧縮、定常状態を考えます。磁気拡散を考慮した誘導方程式より
\[\frac{\partial {\bf B}}{\partial t} = \nabla \times ({\bf v} \times {\bf B}) + \eta \nabla^2 {\bf B} = {\bf 0}\]リコネクション領域の厚みを\(\delta\)として、空間微分を\(\nabla \simeq 1/\delta\)と近似すると
\[\frac{v_i B}{\delta} \simeq \frac{\eta}{\delta^2} B \ \Longrightarrow \ v_i \simeq \frac{\eta}{\delta}\]inflow = outflowより、連続の式から
\[v_i L = v_o \delta\]リコネクション部分において、\(x\)方向の速度が\(v_x=0 \rightarrow v_x = v_o\)まで加速されています。これはガス圧による仕事と考えましょう。エネルギー保存則より
\[\frac{1}{2} \rho v_o^2 = p_i - p_o\]となります。さらにリコネクション中心部においては、磁場が散逸しており\(p_{\rm mag} = 0\)と考えられます。よって内部と外部の全圧力の平衡から
\[p_i \simeq p_o + \frac{B^2}{8\pi}\]エネルギー保存則の式と圧力平衡の式から
\[\frac{1}{2} \rho v_o^2 \simeq \frac{B^2}{8\pi} \ \Longrightarrow \ v_o^2 \simeq \frac{B^2}{4\pi \rho} = v_A^2\]となります。この式と連続の式と誘導方程式より
\[v_i = \frac{\delta}{L}v_A = \frac{v_A}{L}\frac{\eta}{v_i} \ \Longrightarrow \ v_i^2 = \frac{\eta}{L} v_A\]ここで磁気レイノルズ数(magnetic Reynolds number)
\[{\rm R}_m = \frac{v_A L }{\eta}\]を用いて書き換えると
\[v_i = \frac{v_A}{\rm{R}_m^{1/2}}\]inflowの速度\(v_i\)はリコネクションの速さを表すのでリコネクション率と呼ばれます。無次元化されたリコネクション率は
\[M_A = \frac{v_i}{v_A} = {\rm R}_m^{-1/2}\]となります。
エネルギー開放率
この磁気リコネクションによるエネルギー開放率を考えましょう。inflowによる磁場のエネルギーが全てリコネクション領域で消失すると考えると、エネルギー流入率がそのままエネルギー開放率になります。磁場のエネルギー流入率は(磁気エネルギー流速(ポインティングフラックス)) x 面積(\(L^2\))より\(\frac{B^2}{4\pi} v_i L^2\)です。体積\(L^3\)に入っていたエネルギーがこのエネルギー開放率で消失するまでにかかる時間スケールは
\[\tau \simeq \frac{\frac{B^2}{8\pi}L^3}{\frac{B^2}{4\pi}v_i L^2} = \frac{1}{2} \frac{L}{v_i} = \frac{1}{2} \frac{L/v_A}{v_i /v_A} = \frac{1}{2} \frac{t_A}{M_A}\]ここで\(t_A\)はアルヴェーン横断時間(Alfven crossing time, アルヴェーン速度で系を横切るのにかかる時間)です。スウィート・パーカーモデルの場合のエネルギーの開放にかかる時間を\(t_{\rm SP}\)として、係数の2を無視すると
\[t_{\rm SP} \simeq {\rm R}_m^{1/2} t_A = (t_A t_D)^{1/2} = {\rm R}_m^{-1/2} t_D\]となります。ここで\(t_D = L^2/\eta\)は磁気拡散のタイムスケールです。実際の太陽のパラメータを代入してタイムスケールを計算すると以下のようになります。
\[t_{\rm SP} \simeq 10^7 \left( \frac{L}{10^9{\rm cm}}\right)^{3/2} \left( \frac{T}{10^6{\rm K}}\right)^{3/4} \left( \frac{B}{100{\rm G}}\right)^{-1/2} \left( \frac{n}{10^9{\rm cm}^{-3}}\right)^{1/4} [{\rm s}]\]これは実際のフレアのタイムスケール(数分~数時間)よりは十分長いです。
参考文献
[1] 桜井隆, 小島正宣, 小杉健郎, 柴田一成, “シリーズ現代の天文学 太陽”
[2] Priest, “Solar Magnetohydrodynamics”