Table of contents
3. ガスの状態と光の吸収・発光係数
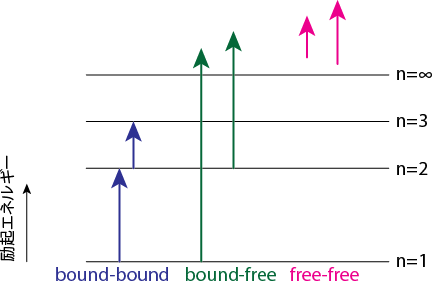
イオンに束縛された電子または自由電子による光の吸収・発光は束縛状態のエネルギー準位間のBound-bound遷移、束縛状態と自由状態間のBound-free遷移(電離または再結合)、自由状態間のFree-free遷移に伴って起こります。Bound-bound遷移は線吸収・発光を起こし、Bound-freeとFree-free遷移は連続吸収・発光を起こします。
3.1 Bound-bound遷移に対するEinstein係数
Esinstein係数
最初に2つのレベル間で起こるBound-Bound吸収について考察しましょう。下のレベルを\(l\)、上のレベルを\(u\)とし、それぞれの状態の統計的重率をそれぞれ\(g_l, g_u\)と書きます。また、それぞれのレベルにある原子の数密度をそれぞれ\(n_l, n_u\)とします。
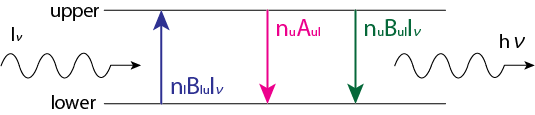
Intensity \(I_\nu\)の光を吸収して、レベル\(l\)からレベル\(u\)に遷移が起こる確率は
\[n_l B_{lu} I_\nu \frac{d\Omega}{4\pi} \tag{3.1}\]のように書けます。ここで\(B_{lu}\)はEinstein係数の1つで、\(d\Omega\)は微小立体角を表します。この過程におけるエネルギー吸収率は
\[\rho \bar{\kappa}_{lu} I_\nu = n_l \frac{B_{lu} h\nu}{4\pi} I_\nu \tag{3.2}\]のようになります。ここで\(\bar{\kappa}_{lu}\)はこの過程による吸収係数(単位質量あたり)であり、吸収される振動数\(\nu\)は2つのレベルのエネルギー差と\(E_u-E_l = h\nu\)の関係にあります。
上のレベルから下のレベルへの遷移には2つの過程が考えられます。その1つは自然発生的に起こる自発遷移(Spontaneous transition)です。その遷移確率をEinstein係数の1つ\(A_{ul}\)で表すと、自発放射(Spontaneous emission)によるエネルギー放出率(単位立体角あたり)は
のように表されます。もう1つの過程はInduced emission(誘導放射またはStimulated emission)です。遷移によって出る光子と同じエネルギーを持つ光子の存在に誘発されて起こります。その遷移率は同じ振動数の入射光Intensity \(I_\nu\)に比例するので、エネルギー放出率は
\[\rho \eta_\nu (\mathrm{induced}) = n_u \frac{B_{ul} h\nu}{4\pi} I_\nu \tag{3.4}\]のように書かれます。ここで\(B_{ul}\)はEinstein係数の1つです。誘導放射で放出された光の角度依存性は入射光と全く同じであるのに対して、自発放射は等方的に起こります。
Einstein関係式
熱平衡状態では\(I_\nu = B_\nu\)であり、\(n_l\)と\(n_u\)にはBoltzmann関係
\[\left( \frac{n_u}{n_l} \right)^\ast = \frac{g_u}{g_l} e^{-\frac{h\nu}{k_B T}} \tag{3.5}\]があります。\(\ast\)は熱平衡状態での量であることを表すためにつけてあります。上下の遷移が釣り合っていなくてはならないので
\[n_l B_{lu} B_\nu = n_u^\ast A_{ul} + n_u^\ast B_{ul} B_\nu \tag{3.6}\]という関係が成り立ちます。これを\(B_\nu\)について解いて、(3.5)式を使うと
\[B_\nu = \frac{n_u^\ast A_{ul}}{n_l^\ast B_{lu} - n_u^\ast B_{ul}} = \frac{A_{ul}}{B_{ul}} \left( \frac{g_l B_{lu}}{g_u B_{ul}} e^{\frac{h\nu}{k_B T}} - 1\right)^{-1} \tag{3.7}\]一方、Planck関数\(B_\nu\)は以下で与えられるのでした。
\[B_\nu = \frac{2h\nu^3}{c^2} \left( e^{\frac{h\nu}{k_B T}} -1 \right)^{-1} \tag{3.8}\]よって、(3.7), (3.8)式を比較すると以下の2つの関係を得ることができます。
\[A_{ul} = \frac{2h\nu^3}{c^2} B_{ul} \tag{3.9}\] \[g_l B_{lu} = g_u B_{ul} \tag{3.10}\]これらの関係はEinstein relationsとして知られています。この関係式を導出するために熱平衡を仮定しましたが、Einstein relationsは温度に依存しない原子間の性質を表すものです。よって熱平衡であるかないかに関わらず成り立つ関係式です。
2準位間の遷移のみを考えた場合のRadiative transfer equation
2つのレベル間の遷移だけが起こるとした場合を考えましょう。散乱を無視\((\sigma_\nu = 0)\)したRadiative transfer equationは(3.2), (3.3), (3.4)式から
\[\begin{align} \mu \frac{d I_\nu}{dz} &= \rho \eta_\nu - (\kappa_\nu + \sigma_\nu) \rho I_\nu = n_u \frac{A_{ul} h\nu}{4\pi} + n_u \frac{B_{ul} h \nu}{4\pi} I_\nu - n_l \frac{B_{lu} h\nu}{4\pi} I_\nu \notag \\ &= \frac{h\nu}{4\pi} n_u A_{ul} - \frac{h\nu}{4\pi} (n_l B_{lu}-n_u B_{ul}) I_\nu \tag{3.11} \end{align}\]のように書くことができます。上式より\(I_\nu\)に比例する項はInduced emissionを考慮に入れた(Induced emissionは負の吸収と考えます)吸収係数を
\[\rho \kappa_\nu = \frac{h\nu}{4\pi} (n_l B_{lu}-n_u B_{ul}) = \frac{h\nu}{4\pi} n_l B_{lu} \left( 1- \frac{n_u B_{ul}}{n_l B_{lu}} \right) \underbrace{=}_{(3.10)} \frac{h\nu}{4\pi} n_l B_{lu} ( 1- \underbrace{\frac{g_l n_u }{g_u n_l}}_{負の吸収} ) \tag{3.12}\]と見なすことができます。実査にはエネルギー準位が有限の幅を持つことからくる線輪郭関数\(\phi (\nu)\)がかかりますが、ここでは省略しています\((\int\phi(\nu) d\nu = 1)\)。このとき、Source functionは
\[S_\nu = \frac{\eta_\nu}{\kappa_\nu + \underbrace{\sigma_\nu}_{=0}} \underbrace{=}_{(3.11)} \frac{n_u A_{ul}}{n_l B_{lu} -n_u B_{ul}} = \frac{\frac{A_{ul}}{B_{ul}}}{\frac{n_l B_{lu}}{n_u B_{ul}}-1} \underbrace{=}_{(3.9), (3.10)} \frac{2h\nu^3}{c^2} \left( \frac{g_u n_l}{g_l n_u} - 1\right)^{-1} \tag{3.13}\]となります。吸収係数(3.12)は熱平衡のとき、ボルツマン関係(3.5)式より
\[\rho \kappa_\nu = n_l B_{lu} (1-e^{-\frac{h\nu}{k_B T}}) \frac{h \nu}{4\pi} \tag{3.14}\]ここで\((1-e^{-\frac{h\nu}{k_B T}})\)は熱平衡におけるInduced emissionが吸収係数に及ぼす効果を表しています。\(T\)が大きいとIndueced emissionはほとんど影響しませんが、\(\nu\)が小さい(波長が長い)と影響が出てきます。
また熱平衡の時のSouce functionは
のようにPlanck関数に一致します。
メーザー
恒星内部では起こりませんが、強い非熱平衡状態ではPopulation inversion(存在率の逆転); \((n_u/g_u) > (n_l / g_l)\)が起こります。このときは(3.12)式からわかるように、誘導放射の方が吸収よりも大きくなり、吸収係数が負となります。その結果、その領域を通過する光は吸収されるのではなく、強められることになります。この現象はMaser (Microwave Amplification by Stimulated Emission of Radiation)やLaser(Light Amplification by Stimulated Emission of Radiation)として知られます。
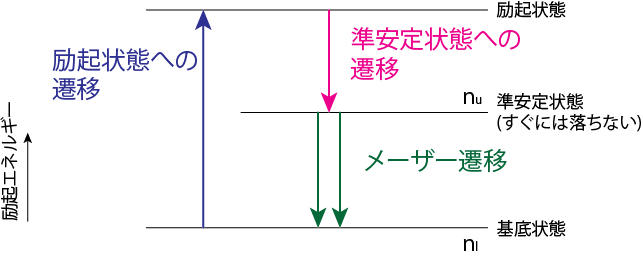
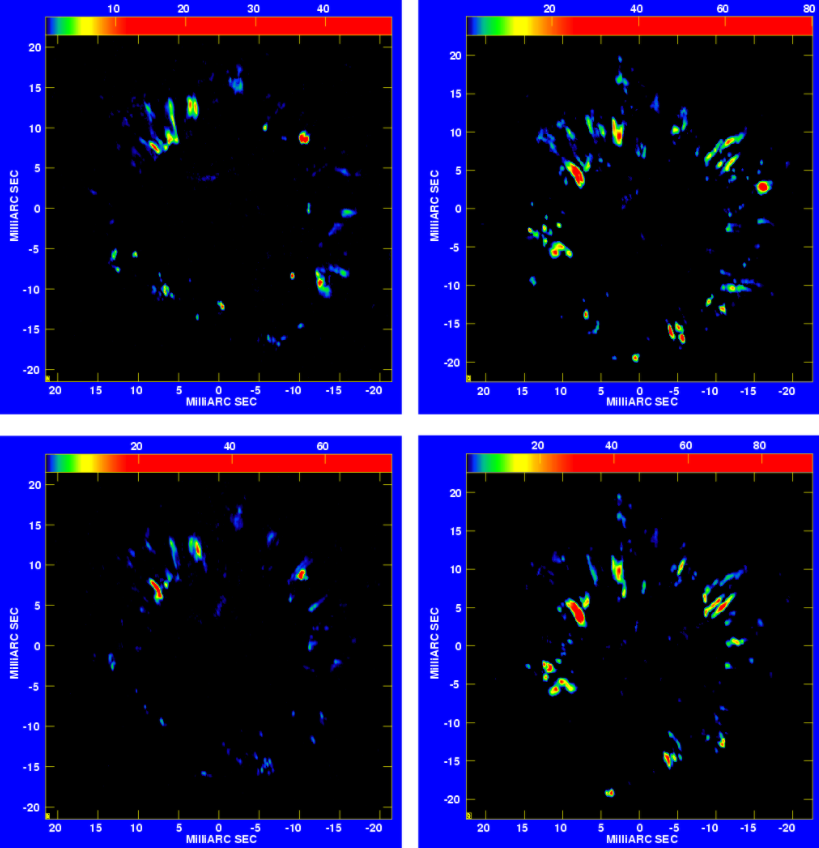
低温・高密度・古い恒星の周星物質ではメーザーがよく見られます。これを用いるとガスの運動などがわかることから、脈動の様子などを調べることができます。
参考文献