Table of contents
速度場と輻射場の性質
運動する点電荷が作る電磁場の性質を考えましょう。
速度場
電場の式のうちの第一項
\[\mathbf{E} (\mathbf{r}, t) = q\left[ \frac{(1-\beta^2)(\mathbf{n}- \boldsymbol{\beta})}{\kappa^3 R^2} \right] \tag{1}\]を速度場と呼びます。点電荷が等速度運動しているときの電場の様子を示してみましょう。
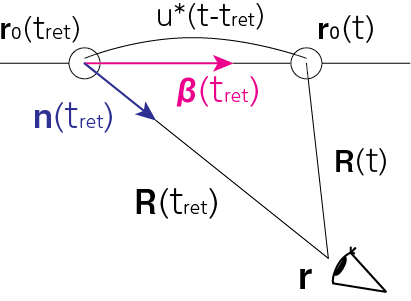
\([\dot{\boldsymbol{\beta}}] = \mathbf{0}\)のとき、\(t-t_\mathrm{ret} = R(t_\mathrm{ret})/c\)より点電荷は電磁波が観測者の位置\(\mathbf{r}\)に到達するまでに\(\frac{R(t_\mathrm{ret})}{c} \mathbf{u}\)だけ移動します。よって
\[\mathbf{R} (t) = \mathbf{r}- \mathbf{r}_0 (t) = \mathbf{r} - \left( \mathbf{r}_0(t_\mathrm{ret}) + \frac{R(t_\mathrm{ret})}{c} \mathbf{u}\right) = \mathbf{R}(t_\mathrm{ret}) -R(t_\mathrm{ret}) \boldsymbol{\beta} = R(t_\mathrm{ret}) (\mathbf{n}(t_\mathrm{ret})- \boldsymbol{\beta}) \underbrace{=}_{等速度より\boldsymbol{\beta} = [\boldsymbol{\beta}]} [R(\mathbf{n}- \boldsymbol{\beta})]\]これより
\[\mathbf{E} (\mathbf{r}, t) \parallel \mathbf{R}(t)\]となり、時刻\(t_\mathrm{ret}\)に等速直線運動をする点電荷から発せられた電磁波の電場は、時刻\(t\)に電荷がいる位置と観測者を結んだ直線に平行となります。あたかも、速度場が速度無限大で観測者のところまで伝播したかのような(遠隔相互作用のような)錯覚を受けることになります。
輻射場
電場の式のうち、第二項
\[\mathbf{E} (\mathbf{r}, t) = \frac{q}{c} \left[ \frac{\mathbf{n} \times \{ (\mathbf{n} - \boldsymbol{\beta}) \times \dot{\boldsymbol{\beta}}\}}{\kappa^3 R}\right] \tag{2}\]を輻射場と呼びます。輻射ばの性質を見ていきましょう。
輻射場の向き
(2)式の形から、輻射場ベクトルは\(\mathbf{n}, \mathbf{n}-\boldsymbol{\beta} \times \dot{\boldsymbol{\beta}}\)に直行します。また非相対論的極限\(\boldsymbol{\beta} = \mathbf{u}/c \rightarrow \mathbf{0}, \kappa \rightarrow 1\)では
\[\mathbf{E}(\mathbf{r}, t) = \frac{q}{c} \left[ \frac{\mathbf{n} \times (\mathbf{n} \times \dot{\boldsymbol{\beta}})}{R}\right] = \frac{q}{c}\left[ \frac{(\mathbf{n} \cdot \dot{\boldsymbol{\beta}}) \mathbf{n} - \dot{\boldsymbol{\beta}}}{R}\right] \tag{3}\]よって、非相対論的極限では輻射場ベクトルは\(\mathbf{n}, \dot{\boldsymbol{\beta}}\)の張る平面内にあることがわかります。
相対論的速度のときの電場の振幅の距離依存性
相対論的な速度で運動する点電荷からの輻射場の振幅が、距離に反比例して減少することを直観的に理解してみましょう。
点電荷が\(x\)軸正方向に速度\(u\)で等速直線運動をしていると考えます。点電荷が原点に到達したところで一定の加速度で減速し、\(\Delta t\)後に静止したとします。減速を始めてから\(t\)後の様子は下図のようになります。
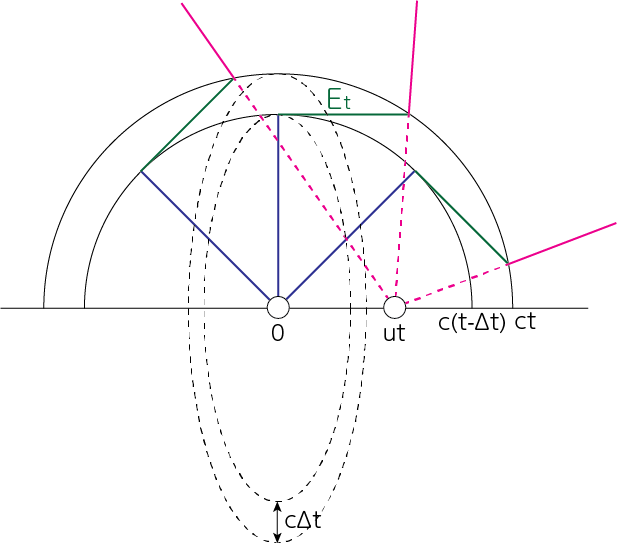
\(\Delta t\)は\(t\)に比べて十分小さいとし、粒子はほぼ原点で静止したとします。半径\(ct\)の球面より外側の領域には、粒子が減速を始めたという情報はまだ伝わっておらず、座標\(ut\)を中心とした放射状に電気力線が分布した速度場のみが存在することになります。一方半径\(c(t-\Delta t)\)の球面の内側では、粒子が静止したという情報が伝わっており、ここには原点を中心とした放射状の速度場のみ存在することになります。この2つの球面に挟まれた球殻状の領域は、減速が起きている間に生成された電磁場が存在する領域となります。系の対称性から、この領域内の電気力線は同一平面内に存在しなければなりません。またこの点電荷以外に電荷が存在しないことから、電気力線は連続でなければなりません。\(\Delta t \ll t\)より、厚さ\(c \Delta t\)の球殻内部の電場は、荷電粒子が原点に静止しているときに発した電場にほぼ垂直であると考えられます。このことは輻射場が横波であることに対応しています。球殻内の電場の球面に沿った成分を\(E_t\)とし、この紙面に垂直で原点を中心に持つような幅\(c \Delta t\)のリングを考えると、このリングを貫く電場は
\[\iint_\mathrm{ring} \mathbf{E} \cdot d\mathbf{S} \simeq 2\pi c t \Delta t E_t\]ただし、\(\Delta t\)は微小なのでリング上で\(E_t = \mathrm{const}\)とすることができます。荷電粒子が1つの系を考えているので、この値は電気力線の連続性から保存する(リングを貫く電気力線の本数は、時間が経過してリングの半径が大きくなろうとも保存する)と考えてよいでしょう。よって
\[2\pi c t \Delta t E_t = {\rm const} \ \Longrightarrow \ E_t \propto \frac{1}{ct} = \frac{1}{R}\]となります。
非相対論的速度のときの電場の振幅
電荷の速度が非相対論的な時の輻射場の電場がどのようになるかを計算してみましょう。(3)式より
\[\begin{align} E (\mathbf{r}, t) &= |\mathbf{E} (\mathbf{r}, t)| = \frac{q}{c} \left[ \frac{| \mathbf{n} \times ( \mathbf{n} \times \dot{\boldsymbol{\beta}}) |}{R} \right] = \frac{q}{c} \left[ \frac{ | \mathbf{n}| | \mathbf{n} \times \dot{\boldsymbol{\beta}} | \sin \frac{\pi}{2}}{R} \right] = \frac{q}{c} \left[ \frac{|\mathbf{n} \times \dot{\boldsymbol{\beta}}|}{R} \right] = \frac{q}{c} \left[ \frac{|\mathbf{n}| |\dot{\boldsymbol{\beta}} | \sin \Theta}{R} \right] \notag \\ &= \frac{q}{c} \left[ \frac{\dot{\beta} \sin \Theta}{R}\right] = \left[ \frac{q \dot{u}}{c^2 R} \sin \Theta \right] \notag \end{align}\]となります。これを物理的考察から導いてみましょう。
点電荷が\(x\)軸正方向に速度\(u(\ll c)\)で等速直線運動しているとします。点電荷が原点に到達したところで一定の加速度で減速し、微小時間\(\Delta t\)後に静止したとします。減速を始めてから\(t\)後の様子は下図のようになります。
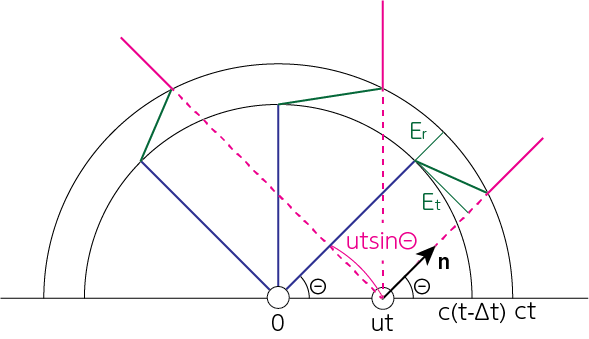
\(u \ll c\)より、半径\(ct\)の球面の外側の電場は半径\(c(t-\Delta t)\)の球面の内側の電場と同じような概形をしていると考えることができます。図のように\(\Theta\)をとると、厚さ\(c \Delta t\)の球殻内部での電場の動径成分\(E_r\)と接線成分\(E_t\)の比は
\[\frac{E_r}{E_t} = \frac{c \Delta t}{ut \sin \Theta}\]です。\(E_r\)の起源は速度場(ただのクーロン電場)であることから
\[E_r = \frac{q}{R^2} = \frac{q}{c^2 t^2}\]よって
\[E_t = \frac{q}{c^3 t} \frac{u}{\Delta t} \sin \Theta \ \stackrel{\Delta t \rightarrow 0}{\longrightarrow} \frac{q}{c^3 t} \dot{u} \sin \Theta = \frac{q \dot{u}}{c^2 R} \sin \Theta\]と求まります。
ポインティングベクトル
ポインティングベクトルの定義\(\mathbf{S} = \frac{c}{4\pi} \mathbf{E} \times \mathbf{B}\)と、輻射場の\(\mathbf{E}, \mathbf{B}\)より
\[\mathbf{S} = \frac{c}{4\pi} [E^2 \mathbf{n}]\]です。
(2)式より\(|\mathbf{S}| \propto R^{-2}\)です。電磁場を放出している点電荷を取り囲む十分に大きい閉曲面\(\Sigma\)を考えると、この閉曲面を通過して外に持ち出される単位時間あたりのエネルギー量は
となります。点電荷から閉曲面までの距離に依存せず一定となることから、輻射場は無限遠方に電磁場のエネルギーを持ち運べることがわかります。輻射場はこの性質ゆえに、輻射場あるいは電磁波と呼ばれています。
さらに電磁場のエネルギー密度\(U = \frac{1}{8\pi} (E^2 + B^2)\)より、輻射場のエネルギー密度は\(U = \frac{1}{4\pi} E^2\)となります。これらから
と書けるため、確かにポインティングベクトルがエネルギー流束になっていることがわかります。
運動量密度
同様に輻射場の運動量密度を計算しましょう。
\[\mathbf{g} = \frac{1}{4\pi c} \mathbf{E} \times \mathbf{B} \ \Longrightarrow \ g = \frac{1}{4\pi c} |\mathbf{E} \times \mathbf{B}| = \frac{1}{4\pi c} E^2\]よって
\[g = \frac{U}{c}\]となり、電磁波の運動量はエネルギーの\(1/c\)であることがわかります。
参考文献
[1] 観山正見, 二間瀬敏史, 野本憲一, “天体物理学の基礎 II”
[2] Rybicki & Lightman, “Radiative Processes in Astrophysics”
[3] 中村文隆, 鶴剛, 長田哲也, 藤沢健太, 梅村雅之, 福江純, “放射素過程の基礎”