Table of contents
Synchrotron energy minimum
ランダム磁場を持つ天体からのSynchrotron平均強度
磁場の方向がランダムに向いて分布している天体からのSynchrotron放射を考えましょう。このとき視線方向と磁場の方向の関係は、\(4\pi\)ステラジアン全ての可能性が現れます。したがって、この天体からのSynchrotron放射強度は、天体を観測する方向に依存せず等方的です。よってスペクトルの厳密な導出で得た視線方向に対して平均化された放射強度が、実際に観測される放射強度となります。電子に対して垂直な平面内を円運動している場合について行うと
\[P_e (\omega, \mathbf{n}) = \frac{\sqrt{3} e^3 B_\perp N_0 \gamma_0^{p-1}}{8\pi^2 m_e c^2(p+1)} \left( \frac{m_ec \omega}{3eB_\perp}\right)^{-\frac{p-1}{2}} \Gamma \left( \frac{p}{4}+ \frac{19}{12} \right) \Gamma \left( \frac{p}{4} - \frac{1}{12}\right) \tag{1}\]を得たのでした。ここで電子は
\[N(\gamma) d\gamma = N_0 \left( \frac{\gamma}{\gamma_0}\right)^{-p} \frac{d\gamma}{\gamma_0} \tag{2}\]で与えられるべき乗型(power law)のエネルギー分布をしているとしました。電子の運動が等方的とすると、磁場に対して様々なピッチ角\(\alpha\)の電子からの放射の平均を観測していることになります。ピッチ角\(\alpha\)の電子からの放射は(1)式において\(B_\perp = B \sin \alpha\)のようにすることで考えることができます。このようにして得られた式に\(\frac{1}{4\pi} \sin \alpha d\alpha \times 2\pi\)をかけて積分することにより平均化され、等方的な分布をした電子からの放射強度が得られます(ここで\(P_e\)が方位角\(\phi\)には依存しないことから、方位角方向の積分は\(2\pi\)に置き換えました)。
sin^nの積分公式より
を用いると、電子のピッチ角に対して平均化された単位周波数あたりの放射強度は
\[\epsilon_\nu = \frac{\sqrt{3} e^3 N_0 \gamma^{p-1}}{4\pi m_e c^2} a(p) \left( \frac{3e}{2\pi m_e c}\right)^{\frac{p-1}{2}} B^{\frac{p+1}{2}} \nu^{-\frac{p-1}{2}} \tag{4}\] \[a(p) \equiv \frac{\sqrt{\pi} \Gamma \left( \frac{p}{4} + \frac{19}{12} \right) \Gamma \left( \frac{p}{4} - \frac{1}{12} \right) \Gamma \left( \frac{p+6}{4}\right)}{2 (p+1) \Gamma \left( \frac{p+8}{4}\right)} \tag{5}\]のように求まります。ここで変数を各周波数から周波数へと変換するのに\(\epsilon_\omega d\omega = \epsilon_\nu d\nu\)を用いました。(2)式の電子数のべき乗分布の式が単位体積あたりの電子数を与えるとすれば、\(\epsilon_\nu\)は単位体積あたりのシンクロトロン放射強度を与えます。天体の体積を\(V\)、天体の平均磁場強度と相対論的電子数密度が天体内部で一様とすると、この天体からの周波数\(\nu\)における全放射強度は
\[L_\nu = \epsilon_\nu V \tag{6}\]で与えられます。
物理量の縮退とエネルギー最小状態を用いた議論
Synchrotron放射は磁場強度と相対論的電子の個数密度の積に比例しています。よってSynchrotron放射強度の測定のみからでは天体の磁場強度と相対論的電子の個数密度がそれぞれどのような割合になっているかは知ることができません(磁場強度と相対論的電子数密度が縮退しています)。そこでエネルギー最小値(energy minimum)の議論を用いてSynchrotron放射強度の測定結果のみから、これらの2つの情報を引き出す方法を以下の手順で求めてみましょう。
天体内の相対論的電子の全エネルギーは、電子1個の全エネルギーが\(\gamma m_e c^2\)より
と与えられます。ここでは磁場の依存性がわかるように書いています。
観測から決定されるSynchrotron全放射強度\(L_\nu\)を一定に保ち、相対論的電子と磁場の全エネルギー
を最小にする状態を考えましょう。この\(W_\mathrm{tot}\)は(9)式の形から、以下の図のように極小値(=最小値)を持つことが予想されます。
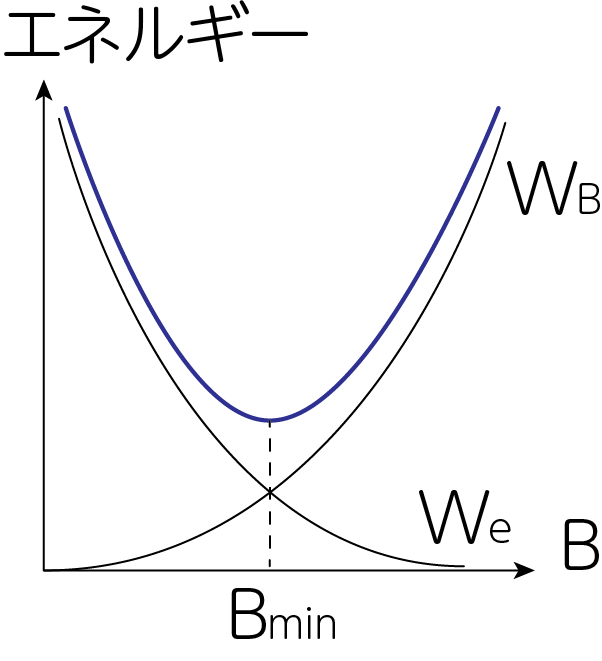
最小値となる状態では、その微分が0より
\[\frac{\partial W_\mathrm{tot}}{\partial B} = - \frac{p+1}{2} G(p, \nu ) L_\nu B^{-\frac{p+3}{2}} + \frac{V}{4\pi} B = 0 \ \Longrightarrow \ B_\mathrm{min} = \left( \frac{2\pi (p+1) G(p, \nu) L_\nu}{V} \right)^{\frac{2}{p+5}} \tag{10}\]\(B = B_\mathrm{min}\)のとき
\[\begin{align} W_e &= G(p, \nu ) L_\nu \left( \frac{2\pi (p+1) G(p, \nu) L_\nu}{V} \right)^{-\frac{p+1}{p+5}} = G(p, \nu )^{\frac{4}{p+5}} L_\nu^{\frac{4}{p+5}} \left( \frac{2\pi (p+1)}{V} \right)^{-\frac{p+1}{p+5}} \notag \\ &= \left( \frac{2\pi (p+1)}{V} \right)^{-\frac{p+1}{p+5}} \left( \frac{2\pi (p+1)}{V}\right)^{-\frac{4}{p+5}} \underbrace{\left( \frac{2\pi (p+1) G(p, \nu )L_\nu}{V} \right)^{\frac{4}{p+5}}}_{=B_{\rm min}^2} = \frac{V}{2\pi (p+1)} B_\mathrm{min}^2 \notag \\ &= \frac{4}{p+1} W_B \quad \left( W_B = \frac{B_\mathrm{min}^2}{8\pi} V \right) \tag{11} \end{align}\]となります。(10)式から、\(L_\nu\)を観測から求めることで磁場強度\(B_\mathrm{min}\)を求めることが可能です。
実際の観測例とJy単位
実際に銀河団の典型的な値から\(L_\nu\)およびflux密度
\[F_\nu = \frac{L_\nu}{4\pi r^2} \tag{12}\]がどの程度の大きさになるかを見てみましょう。銀河団の典型的な値として\(B = B_\mathrm{min}=1 \mu \mathrm{G}\)、銀河団を半径1Mpcの球状天体、そして観測者からこの銀河団までの距離を\(r = 100\)Mpcとします。また観測周波数を\(\nu = 1\mathrm{GHz}\)とします。また相対論的電子の分布として\(p=3, \gamma_1 = 10^2, \gamma_2=10^5\)とします。
(7), (11), (12)式より
種々の値を代入して具体的な数値を求めましょう。
\[G(3, 1\mathrm{GHz}) = \frac{4\pi(m_ec^2)^2}{\sqrt{3}e^3} \left( \frac{3e}{2\pi m_e c}\right)^{-1}\frac{1}{a(3)} (10^{-2}- 10^{-5}) \ 1 \mathrm{GHz} = \frac{8\pi^2 }{3\sqrt{3} a(3) }\frac{(m_ec^2)^3}{e^4 c} (10^{-2}- 10^{-5}) 10^9 \mathrm{Hz}\]途中に現れた量は
\[\begin{align} \frac{(m_e c^2)^3}{e^4 c} &= \frac{(m_e c^2)^3}{\left( \frac{e^2}{\hbar c}\right)^2 (\hbar c)^2 c} \sim \frac{(500 \mathrm{keV})^3}{ \left(\frac{200 \mathrm{MeV \cdot fm}}{140} \right)^2 3 \times 10^{10} \mathrm{cm}} = \frac{125 \times 10^{15} \mathrm{eV}^3}{\left( \frac{10}{7} \times 10^{-7} \mathrm{eV \ cm}\right)^2 3 \times 10^{10} \mathrm{cm}} \notag \\ &= \frac{49 \times 125 }{3} \times 10^{17} \ [\mathrm{eV \ cm^{-3} \ s}] \notag \end{align}\] \[a(3) = \frac{\sqrt{\pi}}{2} \frac{\Gamma \left( \frac{7}{3}\right) \Gamma \left( \frac{2}{3}\right) \Gamma(2)}{4 \Gamma\left(\frac{5}{2}\right)} \underbrace{=}_{\Gamma\left(\frac{5}{2}\right) = \frac{3}{4} \sqrt{\pi}} \frac{\Gamma \left( \frac{7}{3}\right) \Gamma \left( \frac{2}{3}\right)}{6} \sim 0.27\]より
\[G(3, 1\mathrm{GHz}) \sim 1.8 \times 10^{17} [\mathrm{erg} \ \mathrm{cm}^{-3}]\]と計算されます。以上より
\[\begin{align} F_\nu &= \frac{\frac{4\pi}{3} (10^6 \times 3 \times 10^{18} \ \mathrm{cm})^3}{8\pi^2 \times 4 \times 1.8 \times 10^{17} \ \mathrm{erg \ cm^{-3}} (100 \times 10^6 \times 3 \times 10^{18} \mathrm{cm})^2 } (10^{-6} \mathrm{G})^4 \sim 2.2 \times 10^{-23} \ [\mathrm{cm^4 \ G^4 \ erg^{-1}}] \notag \\ &\underbrace{=}_\mathrm{G^2 = erg \ cm^{-3}} 2.2 \times 10^{-23} \ [\mathrm{erg \ cm^{-2} \ s^{-1} \ Hz^{-1}}] = 2.2 \ [\mathrm{Jy}] \notag \end{align}\]ここで\(1 \mathrm{Jy} = 10^{-23} \mathrm{erg \ cm^{-2} \ s^{-1} \ Hz^{-1}}\)はJansky(ジャンスキー)は電波天文学でよく用いられる放射強度の単位です。途中の計算はかなり大雑把に片付けましたが、厳密に計算しても同じ程度のオーダーとなるはずです。 下図は実際にJy単位が用いられている観測論文の図です。上段右のカラーコントアにJy単位が用いられています。
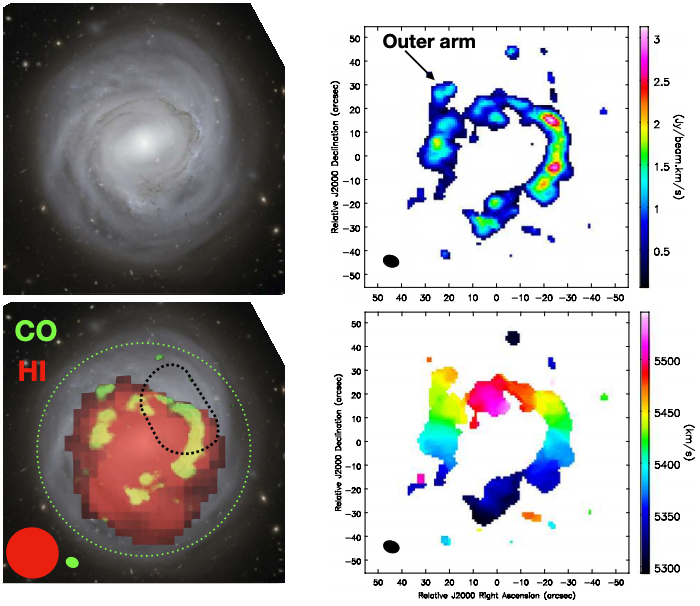
参考文献