Table of contents
電波干渉計の基礎
干渉計がなぜ高分解能の天体画像を得ることができるのか、今回はその原理について勉強しましょう。
干渉計の基礎方程式
干渉計の最も簡単な例として、2つの電波望遠鏡からなる2素子干渉計を考えます。この2つの観測局で、ある電波天体を同時に観測します。 このとき、電波の伝搬速度が有限(光速度\(c\))であるため、電波の同一位相波面が観測局1と2に到達する時刻に差が生じます。この到達時間差を遅延時間と呼びます。遅延時間はアンテナや受信機の内部での機械的遅延及び大気や電離層による伝搬遅延がない理想的な状態では、天体の方向を向く単位ベクトル\(\bf{s}\)と基線ベクトル\(\bf{B}\)の幾何学的な関係のみから決まります。特にこれを幾何学的遅延時間\(\tau_g\)と呼びます。
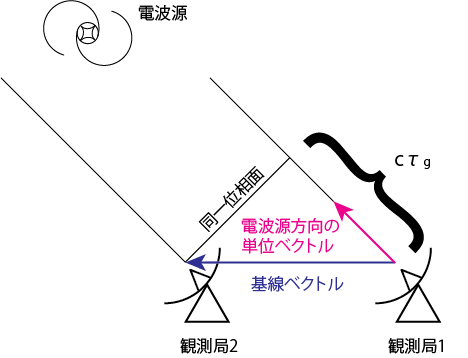
上図から分かる通り、幾何学的遅延時間は
\[\tau_g = \frac{\bf{s} \cdot \bf{B}}{c}\]となります。この遅延時間は干渉計の最も基本的な観測量となります。
幾何学的遅延時間において\(\bf{B}\)が既知の場合、任意の電波源において\(\tau_g\)を計測すると、\(\bf{s}\)を決定することができます。\(\bf{s}\)はベクトル量なので、1回の観測から一意に決定することはできません。しかし、\(\bf{B}\)は地球の回転と共に時事刻々と変化します。時間と共に\(\tau_g\)がどのように変化するかを観測すれば、上式にしたがって天体の方向\(\bf{s}\)を決定することができます。同様に、\(\bf{s}\)が既知の場合には遅延時間\(\tau_g\)の観測から基線ベクトル\(\bf{B}\)を求めることができます。このように天体位置を求める位置天文観測と、基線長を求める測地観測とは、いわば表裏一体の関係にあることがわかります。
相互相関関数
干渉計で遅延時間を計測するには、複数の観測局で受信した信号を曲同士で掛け合わせて、相互相関を取る必要があります。例として先ほどの図のような2素子干渉計において観測された電波の相互相関を考えましょう。
簡単のために天体は点源であるとし、天体からの電波は周波数\(\nu_0\)の単色平面波とします。このとき、観測局1, 2で受診される天体電波(電圧)はそれぞれ
このとき、この2つのシグナルの相互相関関数は
\[R_{12} (\tau) \equiv \lim_{T\rightarrow \infty} \frac{1}{2T} \int_{-T}^T V_1(t) V_2 (t-\tau) dt \tag{1}\]のように定義されます。相互相関関数は観測局1での受信電圧と観測局2での受信電圧を、時間\(\tau\)だけずらしながら掛け合わせることを意味します。
電磁気学などにおいては正弦波的な振動関数を複素数として扱い、必要に応じてその実部をとるやり方を導入すると計算上便利なことがあります。よって先ほどの、各局で観測される電圧も複素数を用いて
と表します。複素電圧を考えた場合の複素相互相関関数は
\[C_{12} (\tau) = \lim_{T \rightarrow \infty} \frac{1}{2T} \int_{-T}^T V_1 (t) V_2^\ast (t-\tau) dt\]以上より、\(C_{12}\)を計算すると
\[C_{12}(\tau) = \lim_{T \rightarrow \infty} \frac{1}{2T} \int_{-T}^T V_0^2 e^{i(2\pi \nu_0 t + \phi)} e^{-i (2\pi \nu_0 (t-\tau-\tau_g) + \phi)} dt = \lim_{T \rightarrow \infty} \frac{1}{2T} \int_{-T}^T V_0^2 e^{2\pi i \nu_0 (\tau + \tau_g)} dt = V_0^2 e^{2\pi i \nu_0 (\tau + \tau_g)}\]を得ます。\(C_{12}\)のうち、振幅が天体電波強度の情報を、位相が遅延時間の情報を持っていることがわかります。このように、複素数で記述された相互相関を複素相互相関関数と呼び、このような処理を行う相関器を複素相関器と呼びます。
パワースペクトル
相関関数をフーリエ変換したものをパワースペクトルと呼びます。パワースペクトルは、どの周波数でどの程度の電力を表すかを表す周波数領域の関数です。フーリエ変換及び逆フーリエ変換は以下で定義されます。
\[X(\nu) = \int_{-\infty}^\infty x(t) e^{-2\pi i \nu t} dt\] \[x(t) = \int_{-\infty}^\infty X(\nu) e^{2\pi i \nu t} d\nu\]フーリエ変換は物理的に同じ現象を時間領域の関数から周波数領域の関数へと変換することを意味しています。相関関数とパワースペクトルも、物理的に同じ現象を時間領域・周波数領域で表したペアです。特に、相互相関関数のフーリエ変換の場合、これをクロスパワースペクトルとも呼びます。
計算例: 単色波の場合
単色波の場合、複素相関関数\(C_{12}(\tau)\)をフーリエ変換します。
\[S (\nu) = \int_{-\infty}^\infty C_{12}(\tau) e^{-2\pi i \nu \tau} d\tau = V_0^2 \int_{-\infty}^\infty e^{2\pi i \nu_0 (\tau + \tau_g)} e^{-2\pi i \nu \tau} d\tau = V_0^2 e^{2\pi i \nu_0 \tau_g} \delta (\nu-\nu_0)\]この式は最初に仮定した通り、周波数\(\nu_0\)の基線スペクトルになっています。またその振幅は電圧の2乗なので、電力に比例します。したがって、相関関数のフーリエ変換が確かにパワースペクトルになっていることがわかります。さらにパワースペクトルの位相項は\(\phi = 2\pi \nu_0 \tau_g\)です。
計算例: 連続波源の場合
上述の例では周波数\(\nu_0\)の単色波を考えました。しかし、連続波のスペクトルの場合、上の式を\(\nu_0\)について周波数方向に積分したものになります。このときのパワースペクトルは
\[S(\nu) = F_\nu e^{2\pi i \nu \tau_g}\]となります。ここで\(F_\nu\)は周波数方向のフラックス分布を表す実関数です。この式より、パワースペクトルの位相\(\phi\)は周波数\(\nu\)の関数として、\(\phi = 2\pi \nu \tau_g\)となっています。
遅延追尾
相互相関を得るためには式(1)で時間積分する間、\(\tau_g\)が一定でなければなりません。しかし、実際の干渉計(特に基線長の大きいVLBI)では地球回転の効果により\(\tau_g\)は時々刻々と変化します。地球回転の角速度は
\[\omega_\oplus = \frac{2\pi}{24 \times 3600 \ {\rm sec}} \sim 7.27 \times 10^{-5} \ [{\rm radian/s}]\]です。基線長の例として、VERAの最長基線である\(B \sim 2300 {\rm km}\)を用いると、基線長の変化率は
\[\dot{\bf B} \simeq |{\bf B}| \omega_\oplus \sim 167 \ [{\rm m/s}]\]となります。よって一秒間に幾何学的遅延時間は100m以上変化します。一方で
\[\phi = 2\pi \nu \tau_g = 2\pi \frac{\bf{B} \cdot \bf{s}}{\lambda}\]より、パワースペクトルの位相の変化率を回転数で表したものは
\[\frac{\dot{\phi}}{2\pi} = \frac{\dot{\bf B} \cdot {\bf s}}{\lambda}\]のようになります。例えばVERAで22GHz帯の観測の場合\(\lambda \sim 1.3 {\rm cm}\)より
\[\frac{\dot{\phi}}{2\pi} \simeq \frac{|{\bf B}| \omega_\oplus }{\lambda} \sim 1.2 \times 10^4 \ [{\rm Hz}]\]となります。よって、この例では相関関数を計算するために仮に1秒間積分したとすると、その間に\(\tau_g\)の変化によって位相が12000回も余計に回転します。これでは正しく積分することは不可能です。このため、相関関数を得るには位相回転を止めるための幾何学的遅延時間\(\tau_g\)を打ち消すような補正高\(-\tau_0\)を加える必要があります。これには、予めわかっている天体の位置をもとに予想したものを用います。この補正を遅延追尾と呼び、\(\tau_0\)の計算に使われる天体の予想位置を追尾中心と呼びます。遅延追尾は、過去にはVLAなどの結合素子化型干渉計では、伝送ケーブルの長さを調節することによって行われてきました。現在では計算機でデジタル的に補正を行います。
遅延追尾を行った場合のパワースペクトルは
となります。遅延追尾が完璧に行われている場合、\(\tau_g = \tau_0\)より位相項は0となります。
UVW座標
地球から追尾中心に向かう方向をW成分、それに直交する成分のうち東向きにU、北向きにVをとるような直交3次元座標系を導入します。そして基線ベクトルを\({\bf B} = (U, V, W)\)と表現します。この座標系では、追尾中心いある天体の方向を向く単位ベクトルは
\[{\bf s}_0 = (0, 0, 1)\]となります。追尾中心からわずかにずれた天体の方向ベクトルについては赤道座標系上\((\alpha, \delta)\)での位置のオフセットを(\Delta \alpha \cos \detla , \Delta \delta) = (x, y)とすると
\[{\bf s} = (x, y, \sqrt{1-(x^2 + y^2)})\]と書けます。このとき追尾中心からずれたところに位置する点源のパワースペクトルの位相項\(\phi\)は
\[\tau_g = \frac{\bf{B} \cdot \bf{s}}{c}, \ \tau_0 = \frac{\bf{B} \cdot \bf{s}_0}{c}\]より
\[\phi = 2\pi \nu (\tau_g - \tau_0) \simeq 2\pi \nu \frac{Ux+Vy}{c}\]となります。ここで\(x, y \ll 1\)より\(\sqrt{1-(x^2 + y^2)} \sim 1\)と近似しました。さらに波長\(\lambda = c/ \nu\)で規格化した\(u \equiv U/\lambda, v \equiv V/ \lambda\)を用いると
\[\phi = 2\pi (ux+vy)\]と書くことができます。すなわち、位相項を天体位置のオフセット量\(x, y\)とUV座標\(u, v\)で表すことができます。\(U, V\)は、天体から地球上の観測局を見たときに、その視線に垂直な面に地球上の観測局位置を投影したものです。よって地球回転と共に時々刻々と変化します。\(UV\)面状を地球回転に伴って基線ベクトルが動くことで生じる軌跡をUV Coverageと言います。
上で得られた位相を用いて、パワースペクトルを改めて書き直しましょう。
このようにパワースペクトルを\((u, v)\)の関数として表したものを、特にビジビリティ(Visibility)と呼びます。
像合成
これまでの議論では天体が点源であることを仮定しましたが、以下では天体が点源ではなく、広がった構造を持っている状態を考えます。
そのために、天体の構造を点源の重ね合わせで表すとします。フラックス\(F_i\)の点源が位置\((x_i, y_i)\)にあるとき、観測されるパワースペクトルはそれらの重ね合わせとなります。よって
となります。あるいはスムーズな輝度分布\(I_\nu (x, y)\)を考えると、フラックスと輝度の関係\(F(x, y) = I_\nu (x, y) dx dy\)を用いて
\[S(\nu) = \sum_i I_\nu (x_i, y_i) e^{2\pi i (u x_i + v y_i)} dx_i dy_i = \iint I_\nu (x, y) e^{2\pi i (u x + v y)} dx_i dy_i\]となります。これより、パワースペクトルとビジビリティは輝度分布\(I_\nu\)の2次元フーリエ変換(\(x \leftrightarrow u, y \leftrightarrow v\))になっています。すなわち、干渉計観測によって得られるビジビリティを以下のように逆フーリエ変換することで、天体の輝度分布を得ることができます。これが干渉計による像合成の基本原理です。すなわち
\[I_\nu (x, y) = \iint S_\nu (u, v) e^{-2\pi i (ux + vy)} dudv\]です。最後に相互相関関数、パワースペクトルとビジビリティ、そして輝度分布のフーリエ変換を通じた関係をまとめます。
\[C(\tau) \leftrightarrow S(\nu) = S_\nu (u, v) \leftrightarrow I_\nu (x, y)\] \[\tau \leftrightarrow \nu, \ (u, v) \leftrightarrow (x, y)\]ビームパターン
例として、強度1の点源を干渉計で観測した場合にどのように見えるかを考えてみましょう。この場合の輝度分布は
\[I_\nu (x, y) = \delta (x) \delta (y)\]で与えられます。これを2次元フーリエ変換しましょう。
\[S_\nu (u, v) = \iint_{-\infty}^\infty I_\nu (x, y) e^{2\pi i (ux + vy)} dx dy = 1\]となります。よって、強度1の点源を観測した場合のビジビリティはどの(u, v)点でも振幅1, 位相項0となります。これは点源の場合には干渉計の基線長に関係なく、全く同じパワーで観測されることを意味しています。
話は変わり、我々が観測で最初に得る量は\(S_\nu (u, v)\)です。これを2次元フーリエ変換を用いてこれを\(I_\nu (x, y)\)に直して画像を得て、それを天文学研究に利用します。ここでフーリエ変換でビジビリティを輝度に変換する式
\[I_\nu (x, y) = \iint_{-\infty}^\infty S_\nu (u, v) e^{-2\pi i (ux+vy)} du dv\]では暗黙のうちに積分区間が無限大であることを仮定しています。一方で、実際の干渉計は有限の基線長を持つため、干渉計観測でサンプルされる\((u, v)\)領域は有限です。
有限の\((u, v)\)領域が及ぼす観測への影響を見るために、以下で1次元の問題を考えましょう。天体は1次元の点源であるとして、輝度は\(x\)成分、そしてビジビリティは\(u\)成分のみを考えます。そして有限区間\(-u_0 < u < u_0\)で一様にサンプルした状況を考えましょう。ここで\(u_0 \equiv U_0 / \lambda\)であり、\(U_0\)は最大基線長です。以上のもとで観測されるビジビリティは
です。これを逆フーリエ変換して天体の輝度分布を求めると
\[I_{\rm obs} (u) = \int_{-u_0}^{u_0} S_\nu (u) e^{-2\pi i ux} du = \frac{1}{-2\pi i x} \left[ e^{-2\pi i ux} \right]_{-u_0}^{u_0} = \frac{sin (2\pi u_0 x)}{\pi x}\]これはsinc関数(\({\rm sinc} x = \sin x/ x\))の形をしています。これは\(x=0\)に一番近いゼロ点は\(x = 1/(2u_0)\)となります。点源を観測したときの広がり\(x_{\rm beam}\)ははこれを2倍して
\[x_{\rm beam} = \frac{1}{u_0} = \frac{\lambda}{ U_0}\]となります。ここで\(U_0\)は\(U\)の最大値です。この結果から干渉計で点源を観測すると、その広がりは\(\lambda/U_0\)として観測されます。これが干渉計のビームサイズ(分解能)です。この式は単一鏡の分解能を表す式\(\theta_{\rm beam} = \lambda/D\)に相当します(単一鏡の口径\(D\)を最大基線長\(U_0\)で置き換えたものになっています)。またsinc関数の概形から、\(x\)が大きいところでも小さな山谷が繰り返して存在します。これをサイドローブと呼びます。サイドローブがメインビームに対して大きいと、観測されたイメージから真のイメージを推定することが難しくなります。サイドローブをできるだけ小さくするにはUVカバレッジをできるだけよくする他に、観測されたUV点に重みをかけて、動的にビームを制御することもあります。このようにUVに対する重みをかける操作をテーバーと呼びます。例えばテーパー関数としてガウス分布を考えましょう。ガウス分布のフーリ変換はガウス分布なので、サイドローブの大きさをかなり抑制することができます。しかしガウス分布の重みをかけると長基線のデータの重みが小さくなり、結果としてイメージの空間分解能は劣化します。
ミッシングフラックス
干渉計では単一鏡に比べて高い分解能が安静されるのと引き換えに、広がった構造に対する感度が低下するという問題が発生します。これを干渉計によるミッシングフラックスと呼び、干渉計データの解釈にあたっては必ず気をつけなければいけません。
極端な例として、一様輝度\(I_0\)で無限に広がった天体を考えましょう。
これよりビジビリティは
\[S_\nu (u, v) = \iint_{-\infty}^\infty I_\nu (x, y) e^{2\pi i (ux + vy)} dx dy = I_0 \delta (u) \delta (v)\]よって観測されるビジビリティは原点\((u, v) = (0, 0)\)以外では全て0となります。これはこのような天体を干渉計で観測しても、天体が全くないブランクスカイを観測した場合と同じように見えることを意味します。よって一様輝度で無限に広がる構造は、単一鏡(\((u, v) = (0, 0)\)に相当します)以外では観測できません。これは一様輝度の天体の場合、各場所からの電波が場所ごとに異なる遅延時間\(\tau_g\)を持っているために、可干渉性を持った積分ができないことに起因します。有限の大きさを持った天体の場合でも、天体の大きさがビームサイズよりも大きくなると、干渉計で検出されるフラックスは真のフラックスに対して著しく減少します。
このようなミッシングフラックスをなるべく小さくするには、
- 短い基線に加えて、UVカバレッジをよくする
- 単一鏡で全フラックスを測定する
の2つが必要になります。ALMAではこの目的のために日本がACA(Atacama Compact Array)を分担しています。ACAは7m鏡12台の干渉計で短い基線をサンプルすると共に、単一鏡専用の12m鏡4台でミッシングフラックスのないトータルフラックスを測定しています。